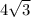 см
см
Объяснение:
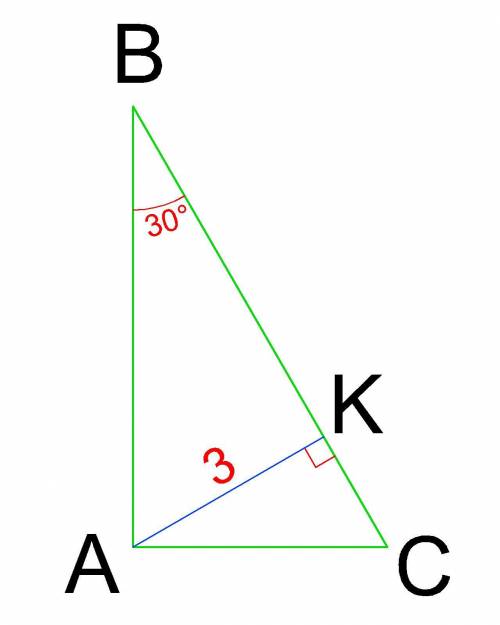
Побудуємо прямокутний ΔАВС, з висотою АК=3 см і гострим ∠В=30°.
І варіант рішення:
1) Розглянемо прямокутний ΔКВА.
Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)
Катет ВК=АК/tg(B) ⇒ BK=3√3 (см)
2) Трикутники АВС, КВА та КАС подібні між собою (за гострим кутом як прямокутні трикутники). Тому
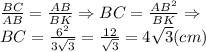
ІІ варіант рішення:
1) Розглянемо прямокутний ΔКВА.
Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)
2) Розглянемо прямокутний ΔКАС.
В ньому ∠С=180°-90°-∠В=60°.
Гіпотенуза АС=АК/sin(С) ⇒ АС=3*2/√3=6/√3 (см)
3) Розглянемо ΔАВС.
Гіпотенуза 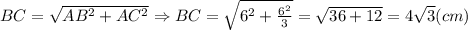
Решение
sin (pi/2+t)-cos(pi-t)+tg(pi-t)+ctg(5pi/2-t) = cost + cost - tgt + tgt =2cost
Объяснение:
sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t). Для упрощения данного выражения используем формулы приведения. По формулам приведения: sin (π/2 + t) = cos t; cos (π - t) = – cos t; tg (π - t) = – tg t; ctg (5π/2 - t) = tg t. Таким образом, мы пришли к выражению: cos t - (– cos t) + (– tg t) + tg t = (раскроем скобки, если перед скобками стоит знак минус "-", то знак слагаемого в скобках необходимо поменять на противоположный) = cos t + cos t - tg t + tg t = (- tg t и tg t взаимно уничтожаются) = 2cos t. ответ: sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t) = 2cos t.