2.48 тік бұрышты үшбұрыштың белгісіз қабырғалары
бурыштарын берілген мәліметтер бойынша табыңдар.
1) екі катеті бойынша:
а) а=3, b=4;
b) a=11, b=60;
ә) a=9, b=10;
г) а=6, b=8;
б) а=20, b=21;
д) a=5, b=12.
с
2) гипотенузасы және катеті бойынша:
а) с=13, a=5;
б) с=17, a=8;
ә) c=25, a=7;
в) с=85, a=84.
3) гипотенузасы және сүйір бұрышы бойынша:
а) с=2, а=20°;
б) с=8, a=70°36';
ә) c=25, а=50°20';
в) с=16, a=76°21'.
4) катеті және оған қарсы жатқан сүйір бұрышы бойынша:
а) а=3, а= 30°27';
б) a=7, а= 60°35';
ә) a=5, а= 40°48';
в) a=9, а= 68°.

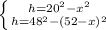
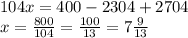
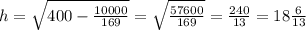
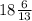
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Доказательство:
Пусть а прямая, перпендикулярная прямым b и c в плоскости . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости .
Проведем произвольную прямую х через точку А в плоскости и покажем, что она перпендикулярна прямой а. Проведем в плоскости произвольную прямую, не проходящую через точку А и пересекающую прямые b, c и х. Пусть точками пересечения будут В, С и Х.
Отложим на прямой а от точки А в разные стороны равные отрезки АА1 и АА2. Треугольник А1СА2 равнобедренный, так как отрезок АС является высотой по условию теоремы и медианой по построению (АА1=АА2). по той же причине треугольник А1ВА2 тоже равнобедренный. Следовательно, треугольники А1ВС и А2ВС равны по трем сторонам.
Из равенства треугольников А1ВС и А2ВС следует равенство углов А1ВХ и А2ВХ и, следовательно равенство треугольников А1ВХ и А2ВХ по двум сторонам и углу между ними. Из равенства сторон А1Х и А2Х этих треугольников заключаем, что треугольник А1ХА2 равнобедренный. Поэтому его медиана ХА является также высотой. А это и значит, что прямая х перпендикулярна а. По определению прямая а перпендикулярна плоскости . Теорема доказана.