ответ: cosA=5√41
Объяснение: если треугольник прямоугольный, то вычислим наибольшую его сторону: АВ; ВС; АС по формуле:
АB²=(Ах-Ау)²+(Ау-Ву)²+(Аz-Bz)²;
AB²=(3-(-4))²+(-5-2)²+(-2-3)²=
=(3+4)²+(-7)²+(-5)²=7²+49+25=49+74=123
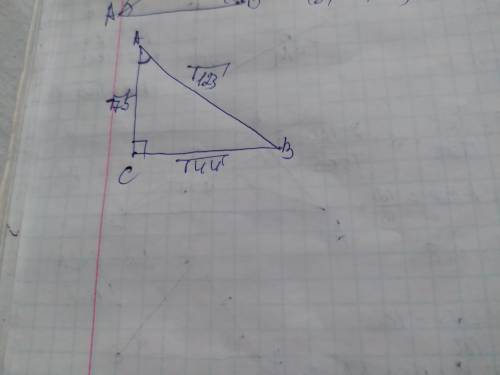
AB=√123=3√41
Остальные стороны найдём по этой же формуле:
BC²=(-4-(-2))²+2-(-4))²+(3-5)²=
=(-4+2)²+(2+4)²+(-2)²=(-2)²+6²+4=4+36+4=44
ВС=√44=2√11
АС²=(3-(-2))²+(-5-(-4))²+(-2-5)²=
=(3+2)²+(-5+4)²+(-7)²=5²+(-1)²+49=25+1+49=
=75; АС=√75=5√3
Итак: АВ=√123=3√41; ВС=√44=2√11;
АС=√75=5√3
Самая большая сторона АВ, значит она и является гипотенузой. Гипотенуза лежит напротив угла 90°, значит этим углом является угол С. Косинус-это отношение прилежащего к углу катета к гипотенузе, поэтому cosA=AC/AB=√75/√123=√(75/123)=
=(√25/41)=5/√41
75 cm2
Объяснение:
Заметим, что треугольники ВОС и DOA подобные. ( по 2-м углам: углы ОВС=ОDA , OCB=OAD - накрест лежащие)
Тогда ВО/DO=CO/AO=2:3
Обозначим СО=2х, тогда АО=3х
ВО=2у, тогда DO=3у
Заметим, что Sabcd=Sboc+Scod+Saod+Sboa
Sboc=(BO*CO*sin BOC)/2=(2x*2y*sin BOC)/2 = 12
4xy*sin BOC=24
xy*sin BOC= 24:4
xy*sin BOC= 6 (1)
Saod=(AO*OD*sinAOD)/2
Так как углы AOD=BOC ( вертикальные), то
Saod= (3x*3y*sinВOС)/2 =9*(x*y*sin ВOС)/2
Подставим согласно (1) вместо x*y*sin ВOС =6, получим
Saod=9*6/2=27 cm2
Scod= (CO*OD*sinCOD)/2
Но углы COD и BOC - смежные, тогда sinCOD=sin(180-BOC)=sinBOC
Тогда запишем:
Scod= (2х*3у*sinВОC)/2 =6*(ху*sinВОC)/2
Опять вместо x*y*sin ВOС подставим 6 согласно (1)
Scod=6*6:2=18 см2
Аналогично Scod находим Saob=(BO*AO*sinBOA)/2=
(2х*3у*sinВОC)/2 =6*(ху*sinВОC)/2 = 6*6:2=18 cm2
Итак Sabcd=Sboc+Scod+Saod+Sboa=12+27+18+18=75см2