1) (1;9); (5;-3); (-3;-5)
2)
Объяснение:
Решение не сложное но довольно таки ёмкое.
Рассмотрим треугольник с вершинами в заданных трёх точках. Для того чтобы четвёртая точка образовала параллелограмм с этими тремя необходимо и достаточно, чтобы эта точка была бы центрально симметрична одной из трёх данных относительно середины отрезка, концами которого являются оставшиеся две. Из чего следует, что данная задача имеет три разных решения, при условии что данные три точки не лежат на одной прямой. Определить координаты четвёртой вершины параллелограмма возможно не менее чем двумя
Находим середину одной из сторон заданного тремя вершинами треугольника и находим координаты четвёртой вершины которая будет концом отрезка чья середина совпадает с уже найденной и другим концом не использованной третей вершины заданного треугольника.
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
I) O(x₁;y₁)-середина TU⇒x₁=(3+(-1))/2=1; y₁=(3+2)/2=2,5
O(x₁;y₁)-середина WV⇒x₁=(x₀+1)/2=1; y₁=(y₀+(-4))/2=2,5
x₀=1; y₀=9
II) O(x₁;y₁)-середина TV⇒x₁=(3+1)/2=2; y₁=(3+(-4))/2=-0,5
O(x₁;y₁)-середина WU⇒x₁=(x₀+(-1))/2=2; y₁=(y₀+2)/2=-0,5
x₀=5; y₀=-3
III) O(x₁;y₁)-середина UV⇒x₁=(-1+1)/2=0; y₁=(2+(-4))/2=-1
O(x₁;y₁)-середина WT⇒x₁=(x₀+3)/2=0; y₁=(y₀+3)/2=-1
x₀=-3; y₀=-5
параллелограмм⇔вектор AB=вектор DC
I) TUVW-параллелограмм⇔вектор TU=вектор WV
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
TU{-1-3;2-3}={-4;-1}, WV{1-x₀;-4-y₀}
{1-x₀;-4-y₀}={-4;-1}⇒x₀=5; y₀=-3
II) TUWV-параллелограмм⇔вектор TU=вектор VW
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
TU{-1-3;2-3}={-4;-1}, VW{x₀-1;y₀+4}
{x₀-1;y₀+4}={-4;-1}⇒x₀=-3; y₀=-5
III) TVUW-параллелограмм⇔вектор TV=вектор WU
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
TV{1-3;-4-3}={-2;-7}, WU{-1-x₀;2-y₀}
{-1-x₀;2-y₀}={-2;-7}⇒x₀=1; y₀=9
Надеюсь, что всё понятно. Если да, то второе задание решите сами.
Используйте оба Одинаковый ответ будет подтверждением правильности ответа.
1. В прямоугольном треугольнике DCE ∠C = 90°, ∠D = 60°, CE = 3 см. Найдите CD и площадь треугольника.
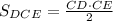
Нужно найти чему равен катет CD.
1) 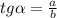 , где а — противолежащий катет, b — прилежащий
, где а — противолежащий катет, b — прилежащий
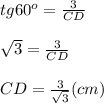
Находим площадь ΔDCE:
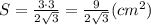
ответ: 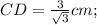
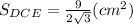
2. В прямоугольном треугольнике PKT ∠T = 90°, KT = 7 см, PT = 7√3 см. Найдите ∠K и гипотенузу треугольника.
По т. Пифагора находим гипотенузу PK:
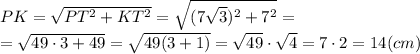
Находит чему равен ∠K
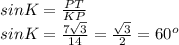
ответ: PT = 14 см; ∠K = 60°.
3. В равнобедренной трапеции меньшее основание равно 8 см, а высота равна √3 см. Найдите площадь трапеции, если один из ее углов равен 150°.
Обозначим трапецию за ABCD, меньшее основание за BC = 8 см, высоты за BH и BH' = √3 см, ∠B = 150° (при меньшем основании).
BCHH' — прямоугольник, образованный основами и высотами. Отрезки BC = HH' = 8 см.
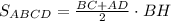
Необходимо найти большее основание AD.
Т.к. трапеция равнобокая, угли при основания равны. Сумма углов выпуклого четырехугольника равна 360°. Поэтому сумма углов при большем основании будет равна:
360−(150°+150°) = 360°−300° = 60°
Значит, угол ∠A = ∠D = 60°/2 = 30°
Р-м ΔABH и ΔDCH': прямоугольные, т.к. образованы высотой трапеции; равные, т.к. трапеция ABCD равнобедренная ⇒ AH = DH'.
Отрезок AH выразим с тангенса угла.

Находим длину большего основания:
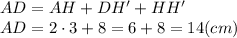
Находим площадь трапеции:
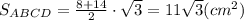
ответ: площадь трапеции 11√3 см².
296°
Объяснение:
центральный равен 1/2 вписанного