Дано :
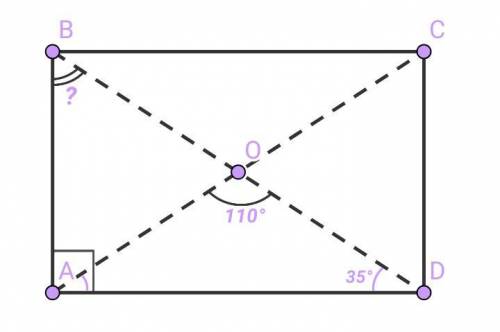
Четырёхугольник ABCD —прямоугольник.
Отрезки АС и BD — диагонали.
Точка О — точка пересечения диагоналей.
Угол AOD = 110°.
Найти :
Угол ABD = ?
Рассмотрим треугольник AOD.
Диагонали прямоугольника точкой пересечения делятся пополам и равны.
Следовательно —
АО = OD.
Тогда треугольник AOD — равнобедренный.
У равнобедренного треугольника углы у основания равны.
Следовательно —
Угол OAD = угол ODA.
По теореме о сумме углов треугольника —
Угол ODA = 0,5*(180° - угол AOD) = 0,5*(180° - 110°) = 0,5*70° = 35°.
Рассмотрим треугольник BAD — прямоугольный (так как угол BAD = 90° по определению прямоугольника).
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно —
Угол ABD = 90° - угол BDA
Угол ABD = 90° - 35° = 55°.
55°.
Відповідь:
3 см
Пояснення:
Відомо, що коло, вписане в трикутник, точками дотику до сторін відділяє рівні відрізки зі сторони кожної вершини.
Також відомо, що висоти - радіуси, проведені із центра такого кола в прямокутному трикутнику до катетів утворюють з відрізками від точок дотику до вершини прямого кута квадрат зі стороною, рівною радіусу вписаного кола.
Згідно з умовою, позначимо AF як 2x, FB як 3x, тоді
r=9-2x
За теоремою Піфагора складемо рівняння:
9²+ (9-2х+3х)²=(2х+3х)²
81+(9+х)²=25х²
81+81+18х+х²-25х²=0
24х²-18х-162=0
4х²-3х-27=0
Дискрімінант: Д=9+4*4*27=441=21²
х₁=(3+21)/8=3 см
х₂=(3-21)/8=-2.25 см (не підходить).
Тоді r=9-2·3=3 см