Если один из внешних углов треугольника острый, то какими являются его остальные внешние углы? надо решение с !

👇

Ответ:

Мадока2000

26.04.2020

тупые
смотри
если внешний острый
то внутренний тупой
угол тругольника
а остальные внешние углы
равны сумме двух не смежных углов

а один из этих не смежных углов -тупой

следовательно и второй внешний угод тупой

ответ: оба тупые

4,4(87 оценок)

Открыть все ответы

Ответ:

alinaLodygina

26.04.2020

Найдите косинус угла В треугольника АВС, если А(2;-4;2), В(3;-3;3), С(4;0;1)

. Векторный (*).

Координаты вектора ВА( -1;-1 ;-1) , вектора ВС(1; 3;-2).

Длины векторов |BA|=√((-1)²+(-1)²+(-1)²)=√3, |BC|=√(1²+3³+(-2)²)=√14 .

cos B= 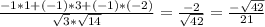$\frac{-1*1+(-1)*3+(-1)*(-2)}{\sqrt{3}*\sqrt{14} } =\frac{-2}{\sqrt{42} } =\frac{-\sqrt{42} }{21}$ .

2 cпособ. По т. косинусов (**).

Для ΔАВС применим т. косинусов: АС²=АВ²+ВС²-2*АВ*ВС*cosВ.

Найдем длины сторон треугольника по формуле расстояния между точками (***) АВ=√( (3-2)²+(-3+4)²+(3-2)² )=√(1+1+1)=√3,

АС=√(2²+4²+(-1)²)=√21, ВС=√(1²+3²+(-2)²)=√14.

Тогда √21²=√3²+√14²-2*√3*√14*cosВ,

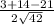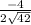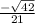cosВ = $\frac{3+14-21}{2\sqrt{42} }$ = $\frac{-4}{2\sqrt{42} }$ = $\frac{-\sqrt{42} }{21}$ .

===================================

(*)Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.

(**)Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

(***)d=√( (х₁-х₂)²+(у₁-у₂)²+ (z₁-z₂)²), где (х₁;у₁; z₁), (х₂;у₂; z₂) -координаты концов отрезка.

4,4(89 оценок)

Ответ:

adventuretime93

26.04.2020

1. Вкажіть формулу відстані між двома точками:
Ответ: В) АВ = (х – х.)+(y, -у)

Обоснование: Формула відстані між точками на площині - це використання теореми Піфагора для сторін прямокутного трикутника, який утворюється між векторами. Якщо А (х1, у1) і В (х2, у2) є координатами двох точок на площині, то сторона АВ прямокутного трикутника має довжину |х2 - х1| і |у2 - у1| по осях x і y відповідно. Застосовуючи теорему Піфагора, отримаємо формулу відстані між точками А і В: АВ = √[(х2 - х1)^2 + (у2 - у1)^2]. Варіант В відповідає цій формулі, тому є правильним.

2. Знайдіть абсолютну величину вектора 4 (-12; 5).
Ответ: Б) 34

Обоснование: Абсолютна величина вектора - це його довжина. Знаходження довжини вектора включає обчислення квадратного кореня суми квадратів його координат. В даному випадку, абсолютна величина вектора 4 (-12; 5) дорівнює √[(-12)^2 + 5^2] = √[144 + 25] = √169 = 13. Варіант Б відповідає цій відповіді, тому є правильним.

3. Дано вектор ті(-6;1) і вектор (5;-3). Знайдіть вектор ті + п.
Ответ: А) (11; 4)

Обоснование: Щоб знайти суму векторів, слід додати їх відповідні координати. Таким чином, вектор ті(-6;1) + вектор (5;-3) буде мати координати (-6 + 5; 1 + (-3)), що дорівнює (11; 4). Варіант А відповідає цій відповіді, тому є правильним.

4. Знайдіть скалярний добуток векторів (2; -3) і (4; -8).
Ответ: A) 32

Обоснование: Скалярний добуток двох векторів визначається як сума добутків їх відповідних координат. Таким чином, скалярний добуток векторів (2; -3) i (4; -8) дорівнює (2 * 4) + (-3 * (-8)) = 8 + 24 = 32. Варіант А відповідає цій відповіді, тому є правильним.

5. Знайдіть координати вектора MN, якщо M(3;-4), N(9; -2).
Ответ: г) (-6; -2)

Обоснование: Щоб знайти координати вектора MN, ми віднімаємо координати точки M від координат точки N. Таким чином, координати вектора MN будуть (9 - 3; -2 - (-4)), або (-6; -2). Варіант г відповідає цій відповіді, тому є правильним.

6. Знайдіть точки перетину прямої 2х - 5у + 20 = 0 з осями координат.
Ответ:
Перетин прямої з осію x: 2х - 5y + 20 = 0
Коли y = 0, ми можемо знайти значення x:
2x - 5(0) + 20 = 0
2x + 20 = 0
2x = -20
x = -10

Тому, точка перетину прямої з осію x: (-10, 0)

Перетин прямої з осію y: 2х - 5у + 20 = 0
Коли x = 0, ми можемо знайти значення y:
2(0) - 5y + 20 = 0
-5y + 20 = 0
-5y = -20
y = 4

Тому, точка перетину прямої з осію y: (0, 4)

7. Знайдіть косинус кута між векторами (1;0) і (0;0,5).
Ответ: А) 1

Обоснование: Формула для обчислення косинуса кута між двома векторами використовує скалярний добуток та абсолютні величини векторів. Косинус кута між двома векторами а дорівнює (а * b) / (|а| * |b|), де а і b - це вектори, а |а| і |b| - це їх абсолютні величини.

У цьому випадку, абсолютна величина вектора (1;0) дорівнює √(1^2 + 0^2) = 1, а абсолютна величина вектора (0;0,5) дорівнює √(0^2 + 0,5^2) = 0,5.

Скалярний добуток векторів (1;0) і (0;0,5) дорівнює (1 * 0) + (0 * 0,5) = 0 + 0 = 0.

Тому, косинус кута між цими векторами (1;0) і (0;0,5) дорівнює 0 / (1 * 0,5) = 0 / 0,5 = 0.

Варіант А відповідає цій відповіді, тому є правильним.

8. Визначте вид чотирикутника ABCD, якщо А(1; 3), В(5;7), С(7;7), D(0; 0).
Ответ: Прямокутник

Обоснование: Щоб з'ясувати, який вид має чотирикутник ABCD, слід звірити продовжені сторони. Якщо протилежні сторони рівні і паралельні, тоді чотирикутник є прямокутником.

У цьому випадку, сторона AB має довжину √[(5 - 1)^2 + (7 - 3)^2] = √[16 + 16] = √32, а сторона CD має довжину √[(0 - 7)^2 + (0 - 7)^2] = √[49 + 49] = √98.

Сторона BC має довжину √[(7 - 5)^2 + (7 - 7)^2] = √[4 + 0] = √4 = 2, а сторона AD має довжину √[(0 - 1)^2 + (0 - 3)^2] = √[1 + 9] = √10.

Таким чином, AB ≠ CD і BC ≠ AD, тому чотирикутник ABCD - прямокутник.

В результаті, чотирикутник ABCD є прямокутником.

4,8(25 оценок)

Это интересно:

Кулинария-и-гостеприимство

23.05.2023

Как использовать галогенную печь: простой и быстрый гид...

19.08.2022

Как выглядеть старше подросткам: советы от экспертов...

Дом-и-сад

16.05.2021

Как заменить шнурки в жалюзи - простой и быстрый способ...

Компьютеры-и-электроника

12.02.2023