Доказательство теоремы Пифагора
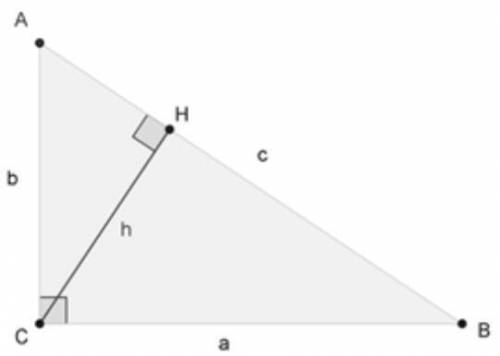
Пусть треугольник ABC - прямоугольный треугольник с прямым углом C
Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H .
Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам ( ∠ACB=∠CHA=90∘∠ACB=∠CHA=90∘, ∠A∠A - общий). Аналогично, треугольник CBH подобен ABC .
Введя обозначения
BC=a,AC=b,AB=cBC=a,AC=b,AB=c
из подобия треугольников получаем, что
ac=HBa,bc=AHbac=HBa,bc=AHb
Отсюда имеем, что
a2=c⋅HB,b2=c⋅AHa2=c⋅HB,b2=c⋅AH
Сложив полученные равенства, получаем
a2+b2=c⋅HB+c⋅AHa2+b2=c⋅HB+c⋅AH
a2+b2=c⋅(HB+AH)
Объяснение:
Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны {\displaystyle a}a и {\displaystyle b}b, а длина гипотенузы — {\displaystyle c}c, выполнено соотношение:
{\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}.
Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в Началах Евклида.
Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением {\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}. Как следствие, для всякой тройки положительных чисел {\displaystyle a}a, {\displaystyle b}b и {\displaystyle c}c, такой, что {\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}, существует прямоугольный треугольник с катетами {\displaystyle a}a и {\displaystyle b}b и гипотенузой {\displaystyle c}c.