ответ: ∠С1А1В1=100°; ∠А1В1С1=48°; ∠В1С1А1=32°
Объяснение:
Треугольник, образованный основаниями высот некоторого треугольника, называется ортотреугольником. .
В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник, подобный данному (теорема).
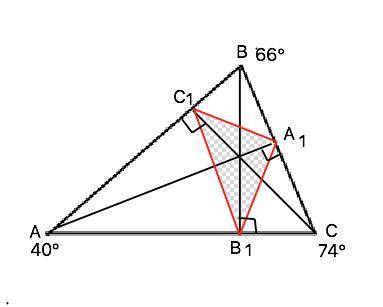
1) ∆ С1ВА1~∆ АВС, ∠ВС1А1=∠С=74°, ∠ВА1С1=∠А=40°
2) ∆ АС1В1~∆ АВС, ∠АС1В1=∠С=74°, ∠ АВ1С1=∠ В=66°
3) ∆А1СВ1~ ∆ АВС, ∠СА1В1=∠А=40°, ∠СВ1А1=∠ В=66°
Основания высот на сторонах ∆ АВС являются вершинами развёрнутых углов
Из угла АС1В -∠В1С1А1=180°-2•74°=32°
Из ВА1С - ∠С1А1В1=180°-2•40°=100°
Из СВ1А - ∠ А1В1С1=180°-2•66°=48°
.
МО - искомая величина.
МА и МВ - наклонные, тогда ОА = 4 см и ОВ = 11 см - их проекции на плоскость α.
Пусть х - коэффициент пропорциональности.
Большая наклонная имеет большую проекцию, поэтому
МА = 2х, МВ = 5х.
Из прямоугольных треугольников МОА и МОВ по теореме Пифагора выразим МО:
МО² = МА² - АО² = 4x² - 16
MO² = MB² - BO² = 25x² - 121
Приравняем правые части равенств:
4x² - 16 = 25x² - 121
21x² = 105
x² = 5
x = √5 (x = - √5 - не подходит по смыслу задачи)
МО = √(4x² - 16) = √(4·5 - 16) = √4 = 2 см