Рассмотрим треугольник NPK.
Угол PKN = 90°, по условию задачи, значит треугольник NPK — прямоугольный. Угол PKN = 90°, угол KNP = 60°. Сумма углов треугольника равна 180°, значит угол NPK = 180° – 90° – 60° = 30°. Одно из свойств прямоугольного треугольника: катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, KN = NP : 2. NP = 2 × KN = 2 × 5 см = 10 см. Воспользуемся теоремой Пифагора (квадрат гипотенузы равен сумме квадратов катетов) и найдем второй катет.
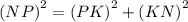
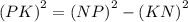
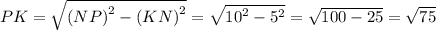 см
см
Рассмотрим треугольник MPK. Идём по тому же пути.
Угол PKM = 90°, по условию задачи, значит треугольник MPK — тоже прямоугольный. Пользуемся тем же свойством прямоугольного треугольника: катет, лежащий против угла в 30°, равен половине гипотенузы. PK = MP : 2. MP = 2 × PK = 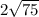 см. Применяем теорему Пифагора и находим катет KM.
см. Применяем теорему Пифагора и находим катет KM.
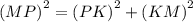
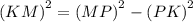
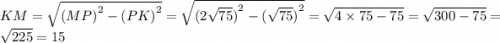 см
см
Объяснение:
№3
Обозначим вершины призмы АВСА₁В₁С₁. Так как призма правильная, то в её основании лежит равносторонний треугольник, поэтому АВ=ВС=АС, а также все боковые грани равны между собой и поскольку площадь основания равна площади одной из боковых граней, то все грани призмы будут равновеликими, и так как граней 5 (3 боковых и 2 грани основания), то площадь каждой грани, а также площадь основания составят:
Sгр.=80√3÷5=16√3(см²).
По формуле площади равностороннего треугольника найдём сторону основания:

где а – сторона треугольника, в нашем случае основания. Перемножим крест накрест:
а²√3=4S
a²√3=4×16√3
a²√3=64√3
a²=64√3÷√3
a²=64
a=√64
a=8(см) – сторона основания
Узнаем высоту призмы АА₁:
АА₁=ВВ₁=СС₁=S÷AC=16√3÷8=2√3(см)
Найдём объем призмы по формуле:
V=Sосн.×АА₁=16√3×2√3=32×3=96(см³)
ОТВЕТ: V=96(см³)
№4
Обозначим вершины призмы АВСДА₁В₁С₁С₁Д₁.
Найдём площадь основания АВСД по формуле:
Sосн=ВС×СД×sinC=4√3×4×sin30°=
=16√3×1/2=8√3(см²).
Сумма углов параллелограмма, прилегающих к одной стороне равна 180°, поэтому ∠В=∠Д=180–∠С=180–30=150°.
Проведём в основании диагональ АС и рассмотрим ∆АВС и найдём АС по теореме косинусов:
АС²=АВ²+ВС²–2×АВ×АС×cos150°=
=4²+(4√3)²–2×4×4√3×(–√3/2)=
=16+16×3+16√3×√3=16+48+16×3=64+48=112АС=√112=4√7(см).
Найдём через тангенс угла высоту СС₁:
СС₁=АС×tg60°=4√7×√3=4√21(см)
V=Sосн×СС₁=8√3×4√21=32√3×√21=
=32√63=32×3√7=96√7(см³)
ОТВЕТ: V=96√7(см³)
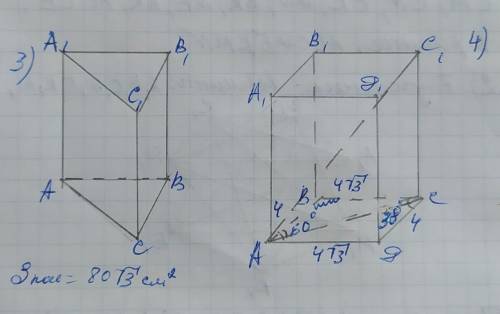
Эта задача на подобные треугольники, которые образуются при пересечении сторон угла ВАС параллельными прямыми (это следы сечения плоскости ВАС плоскостями α и β).
Пусть отрезок А1А2 = х.
Тогда по заданию АА2 = (2/3)х.
Поэтому отрезок АА1 = х + (2/3)х = (5/3)х.
Приравниваем АА1 = 24 = (5/3)х. Отсюда х = 24/(5/3) = 72/5.
АА2 = (2/3)*(72/5) = 48/5 = 9,6.
Отрезок А2В2 находим по коэффициенту подобия к = 18/24 = 3/4.
Тогда А2В2 = 18*(3/4) = 27/2 = 13,5.