а)
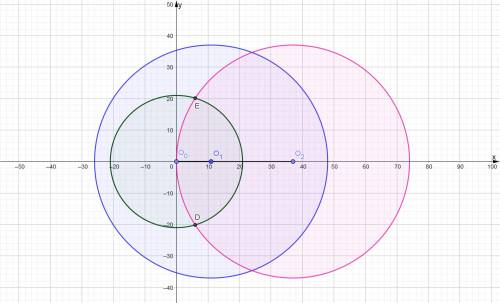
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 11 см, інше коло має бути радіусом (R2) більшим або рівним 10 см ( |R1−d| ) і меншим за 32 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
10 ≤ R2 ≤ 32
Коло з радіусом 37 в даний інтервал довжин не входить, нерівність не виконується ⇒ спільних точок немає.
б)
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 37 см, інше коло має бути радіусом (R2) більшим або рівним 16 см ( |R1−d| ) і меншим за 58 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
16 ≤ R2 ≤ 58
Коло з радіусом 37 в даний інтервал довжин входить, нерівність строга ⇒ спільних точок дві.
Объяснение: 1) ∆ABD=∆ACD по двум сторонам и углу между ними, АВ=АС, <1=<2 по условию, АD общая. Если треугольник и равны, значит <АВD=<ACD=38°, <ADB=<ADC=102° 2) ∆MNE=∆KNF по двум сторонам и углу между ними, MN=NK, EN=NF, углолENM=углуKNF вертикальные. Отсюда ME=KF=8cm., MN=MK÷2=5cm. 3) ∆ABE=∆DCE по двум углам и стороне между ними, AE=ED, <A=<D, <AEB=<CED вертикальные. Отсюда DE=AE=4cm., DC=AB=3cm., EB=EC=5cm. 4) ∆ABC=∆ADC по трём сторонам, AB=AD, BC=DC, AC общая. Значит <BAC=<CAD, отсюда АС биссектриса.