6 ед.
Объяснение:
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.
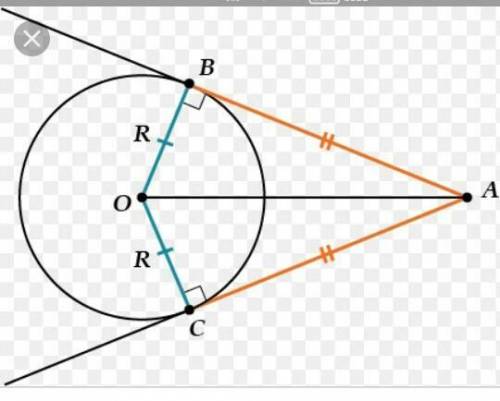
Дано: АВ и АС - касательные, ОА=30 см, ОВ=15 см.
Найти: угол ВОС.
Рассмотрим треуг-ки АОВ и АОС:
ОВ=ОС=R, ОА - общая, АВ=АС (по определению - отрезки касательных, проведенных из одной точки, равны) => эти треугольники равны по 3-му признаку=> уголВОА=угол ОСА.
Рассм. треуг. АОВ: т.к. ОВ в 2 раза меньше АО, то угол ОАВ=30 градусов(сторона, лежащая напротив угла в 30 градусов, равна половине гипотенузы). угол ВОА=180-90-30=60 градусов.
угол ВОС= угол ВОА+ угол ОСА= 60+60=120 градусов.
ответ: 120 градусов.
Дано:
треуг. АВС - р-б
АН - высота
/ВАН = 30°
Найти: /ВАС
тр. АВС равнобедренный -по условию ВС основание =>АН = высота = медиана = биссектриса - по свойству равнобедренного треугольника /ВАН =/НАС - по определению биссектрисы/ВАН=/НАС=30°/ВАС=/ВАН+/НАС=60°