Два перпендикулярных отрезка km и ln пересекаются в общей серединной точке p.
какой величины∡ n и ∡ k, если ∡ l = 10° и ∡ m = 80°?
1. отрезки делятся пополам, значит, kp =
,
= lp,
∡
= ∡ mpl, так как прямые перпендикулярны и оба угла равны
°.
по первому признаку равенства треугольник kpn равен треугольнику mpl.
2. в равных треугольниках соответствующие углы равны.
в этих треугольниках соответствующие ∡
и ∡ m, ∡
и∡ l.
∡ k = °;
∡ n = °.
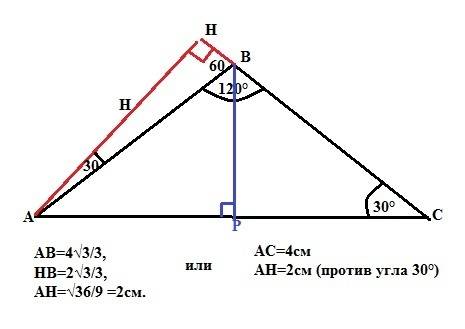
Как известно, площадь треугольника можно вычислить в данном случае по формуле
S=AB*h/2, где h - высота, проведенная к АВ. (1)
Можно вычислить и по-другому.
S=BC*H/2, где H - высота, проведенная к ВС. H надо найти. (2)
Теперь приравняем правые части формул (1) и (2)
AB*h/2=BC*H/2
Умножим обе части на 2, получим
AB*h=BC*H (3)
По условию задачи АВ=16 см, ВС=22 см, h=11 см. Подставим все это в формулу (3)
16*11=22*Н
Сократим обе части на 11
16=2*Н
Сократим обе части на 2
Н=8.
ответ: Н=8 см- высота, проведенная к стороне ВС