Чертёж смотрите во вложении.
Пусть АВ - длина высоты фабричной трубы, ВС - длина высоты тени от фабричной трубы, DE - длина высоты столба, а ЕС - длина высоты тени от столба. Пусть АВ = х.По условию - ВС = 35 м.DE = 7 м.ЕС = 5 м.Рассмотрим прямоугольные ΔАВС и ΔDEC. У них есть общий острый ∠С, поэтому, ΔАВС ~ ΔDEC (по первому признаку подобия прямоугольных треугольников).
В подобных треугольниках против равных углов лежат сходственные стороны.
То есть, DE и АВ - сходственные стороны.
Составим пропорцию и решим её-
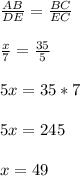
АВ = х = 49 м.
ответ: 49 м.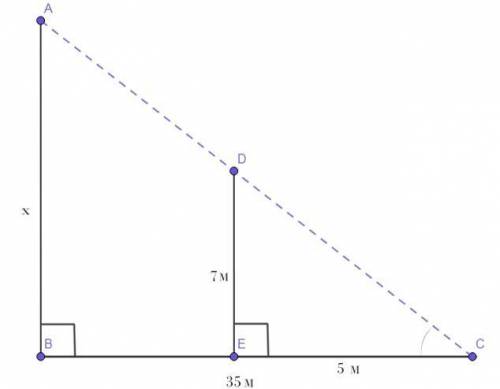
1. Правильный четырехугольник - квадрат. Радиус описанной около квадрата окружности равен половине диагонали.
Если а - сторона квадрата, d - диагональ и R - радиус описанной окружности, то
d = a√2 = 20√2.
R = d/2 = 10√2
2. Центр окружности, описанной около прямоугольника, лежит в точке пересечения его диагоналей. Диагонали прямоугольника равны и являются диаметрами окружности.
По теореме Пифагора:
d = √(12² + 5²) = √(144 + 25) = √169 = 13 см
Длина окружности:
C = πd = 13π см
3. ∠KOD = 30° - центральный угол, значит и градусная мера соответствующей ему дуги тоже 30°.
∪ DK = 30°
∠МОК = 180° ⇒ ∪ MTK = 180°,
∪ MD = 360° - 180° - 30° = 150°
Длина дуги находится по формуле:
С = 2πR · α / 360°
С_dk = 2π · 5 · 30° / 360° = 5π/6 см
C_mtk = 2π · 5 · 180° / 360° = 5π см
C_md = 2π · 5 · 150° / 360° = 25π/6 см
4. Радиус окружности, описанной около правильного шестиугольника, равен стороне шестиугольника:
R = a = 12 см
Центральный угол правильного шестиугольника:
α = 360° / 6 = 60°
Площадь кругового сектора:
S = πR² · α / 360°
S = π · 144 · 60° / 360° = 24π см²
28 см, 12 см.
Объяснение:
Дано: КМРТ - трапеція, МР/КТ=3/7, АВ - середня лінія, АВ=20 см. Знайти МР та КТ.
Середня лінія трапеції дорівнює напівсумі основ.
Нехай МР=3х см, КТ=7х см. Маємо рівняння:
(3х+7х)/2=20
5х=20
х=4
МР=3*4=12 см; КТ=7*4=28 см.