∠САВ=165°
Объяснение:
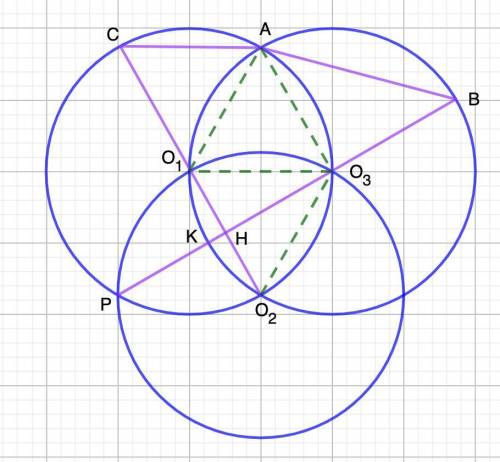
Соединим точки О₁ и А; А и О₃; О₁ и О₃; О₂ и О₃.
Так как три окружности проходят через центры друг друга ⇒их радиусы равны. Пусть радиусы всех окружностей равны R.
1. Рассмотрим Окр. О₁R и Окр. О₂R.
СО₂⊥РО₃ (свойство пересекающихся окружностей)
⇒∠СНВ=90°.
2. Рассмотрим ΔО₁АО₃
О₁А=АО₃=О₃О₁=R
⇒ΔО₁АО₃ - равносторонний.
⇒∠АО₁О₃=60°=∪ АО₃ (центральный)
3. Рассмотрим ΔО₂О₁О₃=равносторонний.
О₁О₃=О₃О₂=О₁О₂=R
⇒∠О₂О₁О₃=60°=∪ О₃О₂ (центральный)
4. ∪ АО₃О₂=∪ АО₃+∪ О₃О₂=60°+60°=120°
5. Рассмотрим Окр. О₁R.
∠О₂СА=120°:2=60° (вписанный)
6. Рассмотрим ΔО₁О₃О₂ равносторонний.
О₃Н⊥РО₃ (п.1)⇒О₃Н-высота, биссектриса (свойство равнобедренного Δ)
⇒∠НО₃О₁=30°=∪ О₁К (центральный)
7. ∠О₁О₃А=60° (ΔО₁АО₃-раввносторонний)
⇒∪ АО₁=∠О₁О₃А=60° (центральный)
8. ∪ КО₁А=∠О₁О₃А+∠КО₃О₁=60°+30°=90°
∠КВА=90°:2=45°(вписанный)
9. Сумма углов четырехугольника равна 360°.
⇒∠САВ=360°-(90°+60°+45°)=165°
Половина основания b/2=а*cos(30)=a*sqr(3)/2, b=a*sqr(3)
Известно, что:
R=a^2/sqr(4a^2-b^2)
Подставив значение b, получим: R=a
Отсюда: АВ=2 см
Во второй задаче центр вписанной окружности совпадает с точкой пересечения биссектрис, поскольку радиусы опущенные из центра в точки М, Т и Р, образуют пары равных прямоугольных треугольников (ВОМ и ВОТ и т.д.). Четырехугольник РОТС является квадратом, так как радиусы проведены в точки касания и перпендикулярны катетам. По условия диагональ этого квадрата равна корень из 8, следовательно сторона будет в корень из двух раз меньше, отсюда:
r=sqr(8/2)=2 Угол ТОР=90 град. Угол ТМР является вписанным, он измеряется половиной дуги, на которую опирается. Дуга составляет 90 градусов, так как ограничена точками Р и Т, а угол РСТ прямой. Следовательно угол ТМР=45 град.