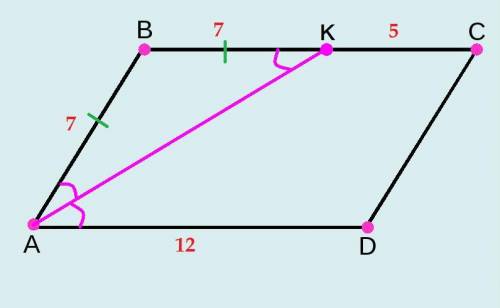
Противолежащие стороны параллелограмма равны (из свойства фигуры параллелограмм).
=> BC=AD=12 (см) => BK=12-5=7 (см).
Так как АК - биссектриса (по условию), то она делит угол А так, что углы ВАК и КАD равны между собой.
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны (из определения).
=> при пересечении двух параллельных прямых секущей накрест лежащие углы равны.
=> угол ВКА = углу КАD, а они накрест лежащие при ВС || АD и секущей АК.
В равнобедренном треугольнике две боковые стороны равны и углы при основании тоже равны (из свойства равнобедренного треугольника).
=> треугольник АВК - равнобедренный (угол ВАК = углу ВКА) и АВ=ВК=7 (см).
Периметр параллелограмма равен удвоенной сумме 2х его соседних сторон (из теоремы о периметре параллелограмма).
=> Р=2*AB+2*AD=2*7+2*12=14+24=38 (см).
ответ: Р параллелограмма АВСD равен 38 (см).
Відповідь:
Площа ромба 96 см2
Пояснення:
Периметр ромба це сума всіх його сторін, а оскільки всі сторони у ромба рівні, то сторона ромба = 10 см. Відома одна діагональ. Оскільки діагоналі ромба дііляться в точці перетину навпіл під прямим кутом, то утворюються 4 рівні прямокутні трикутники. Розглянемо трикутник з відомими двома сторонами 10 см та 12см : 2 = 6см. За теоремою Піфагора знайдемо половину другої діагоналі.
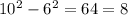
Половина другої діагоналі 8 см, то ж діагональ = 8*2=16 см
Тепер можемо знайти площу ромба за формулою:
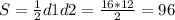
Объяснение:
В первом номере ответ ∠C = 180° - ∠A - ∠B = 180° - ∠B + 21° - ∠B
∠C = 201° - 2∠B
∠C = 201° - 2(∠C - 18)
∠C = 201° - 2∠C + 36°
3∠C = 237°
∠C = 79°
Во втором номере ответ
По теореме синусов:
a/A = b/B = c/C
a/A = b/B = 20/sin75 = b/sin60 = 20/0,9659 = b/0,8660, отсюда b = 20*0,8660/0,9659 = 17,9 ~ 18 см
Угол С = 180° - (75°+60°) = 45°
a/A = c/C
20/0,9659 = c/sin45 = 20/0,9659 = c/0,7071, отсюда с = 20*0,7071/0,9659 = 14,6 ~ 15 см
ответ: 45°; 18 см; 15 см.