1) ВО = 4√15,14 см ≈ 15,564 см; ОС= 4√15,14 см ≈ 15,564 см;
2) ∠ВСА = 25,9°; ∠ВАС = 64,1°;
3) ∠ВОС = 128,2°; ∠ВОА = 51,8°.
Объяснение:
Задание
В прямоугольнике АВСD диагонали АС и ВD пересекаются в точке О.
АВ = 13,6 см
ВС = 28 см
Найти:
1) ВО и ОС
2) ∠ВСА и ∠ВАС
3) ∠ВОС и ∠ВОА.
Решение
1) По теореме Пифагора находим диагональ АС:
АС = √(АВ² + ВС²) = √(13,6²+28²) = √(184,96 + 784) = √968,96 ≈ 31,128 см
2) Так диагонали прямоугольника равны и в точке пересечения делятся пополам, то:
ВО = ОС = АС : 2 = √968,96 : 2 = √(64 · 15,14)/2 = (8√15,14)/2 = 4√15,14 см ≈ 15,564 см
3) Рассмотрим прямоугольный треугольник ВСА (угол В - прямой; АВ и ВС - катеты; АС - гипотенуза).
Рассчитаем синус угла ВАС.
Согласно определению, синус угла - это отношение противолежащего катета к гипотенузе.
Противолежащий катет ВС = 28 см, согласно условию задачи.
Гипотенуза АС = 31,128 см, согласно выполненному расчету.
Следовательно, синус угла ВАС равен:
sin∠ВАС = ВС : АС = 28 : 31,128 ≈ 0,8995
По таблице синусов находим угол, синус которого равен 0,8995:
arcsin 0,8995 ≈ 64,1°
∠ВАС = 64,1°.
4) ∠ВСА = 90°-∠ВАС = 90°-64,1°= 25,9°.
5) Так как ВО = ОС, то треугольник ВОС является равнобедренным и ∠ОВС = ∠ВСО = 25,9°,
следовательно:
∠ВОС = 180°-∠ОВС -∠ВСО = 180°-25,9°-25,9° = 128,2°.
6) Так как углы ВОС и ВОА являются смежными, то:
∠ВОА = 180°-∠ВОС = 180°-128,2°= 51,8°.
1) ВО = 4√15,14 см ≈ 15,564 см; ОС= 4√15,14 см ≈ 15,564 см;
2) ∠ВСА = 25,9°; ∠ВАС = 64,1°;
3) ∠ВОС = 128,2°; ∠ВОА = 51,8°.
6 см
Объяснение:
Радиусы OK и ОМ, проведённые в точки касания хорд с малой окружностью, будут перпендикулярны касательным - хордам АВ и CD. Но также, по свойству диаметра, перпендикулярного хорде, точки К и М будут лежать на серединах отрезков АВ и CD.
АВ=CD=AL+LB=16+4=20см
AK=KB=20/2=10см
KL=KB-LB=10-4=6см
KLMO - квадрат, поскольку все его смежные стороны имеют между собой прямой угол (2 - как радиусы к касательным, 1 - по условию перпендикулярности хорд, и оставшийся тоже получается 90°), и две его смежные стороны ОК и ОМ равны радиусу.
Значит ОМ=KL=6см
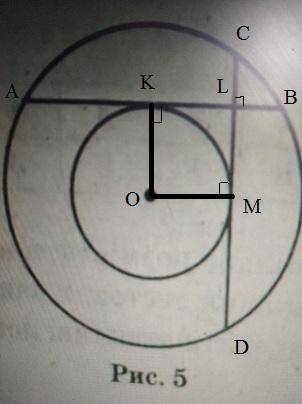
Равенство сторон АВ и CD в данной задаче доказывается через равенство треугольников. Решение задачи с чертежом и доказательством – на рисунке ниже.