Пусть х - проекция первого катета на гипотенузу, у - второго катета.
По условию, x - y = 15 отсюда x = 15 + y.
Высота, проведенная из вершины прямого угла, есть среднее геометрическое между проекциями катетов. Также замечу, что высота h - расстояние от вершины прямого угла до гипотенузы, h = 4.
h² = xy
4² = (15+y)y
y² + 15y - 16 = 0
Решая как квадратное уравнение и принимая во внимая y > 0, найдем искомое значение проекции второго катета y = 1, тогда x = 16. Гипотенуза прям. треуг. равна x + y = 17. Радиус описанной окружности около треугольника равна половине гипотенузы: R = 17/2 = 8,5.
ответ: 5 (метров)
Объяснение: Обозначим высоту дома АВ, высоту фонаря МЕ, расстояние между домом и фонарем АМ ( см. рисунок), место, где лежат зерна, обозначим С.
Т.к. и дом, и фонарь перпендикулярны земле, соединив точки В и Е с точкой С, получим прямоугольные треугольники АВС и СЕМ, гипотенузы которых равны (так как голуби летели с равными скоростями и прилетели одновременно к зерну).⇒ ВС=СЕ
Примем АС=х, тогда СМ=17-х.
ВС²=ВА²+АС²
ЕС²=СМ²+ЕМ²
ВА²+АС²=СМ²+ЕМ²
12²+х²=(17-х)²+5², ⇒ 34х=170, х=5 (метров) = расстояние от дома до зерна.
тр-к АДБ - прямоугольный, т.к. АД - высота
тр-к АДБ подобен тр-ку БАС ( сторона АБ - общая, <Б - общий, <АДБ=<БАС=90°) ⇒
АД = БД = АБ
АБ АС БС,
из тр-ка АДБ найдем БД=√(АБ²-АД²)=√(20²-12²)=√256=16 см
из пропорции подобия найдем АС
АС=АБ*БД/АД=20*16/12=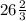
т.к. тр-к АДБ подобен тр-ку БАС, то <С=<БАД ⇒cos<C=cos<БАД = 12/20=3/5
ответ: АС=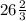
, cos<C= 