Так, подібні. У ромба всі сторони рівні. Якщо провести меншу діагональ, то ми отримаємо ромб, який складається з двох правильних (рівносторонніх) трикутників. Будь-які правильні трикутники подібні (за трьома сторонами). Тому подібними є і конструкції з двох таких трикутників.
P. S. Якщо вже доводити максимально строго: у правильного трикутника кут дорівнює 60°. Тому в цього ромба кути дорівнюють 120°, 60°, 120°, 60°, а всі сторони рівні. Якщо у двох чотирикутників рівні всі відповідні кути, а відповідні сторони пропорційні, то вони подібні.
Объяснение:
1. Сумма углов выпуклого многоугольника равна 180°*(n-1), где n -
количество углов выпуклого многоугольника.
S=180°*(7-2)=180°*5=900°.
2. S=6*7=42 (cм²).
3. S=180°*(13-2)=180°*11=1980°.
4. 15*7=105 (cм²).
5. S=ah/2 h=2S/a=2*45/18=90/18=5 (cм).
6. (1/2) основания = √(15²-9²)=√(225-81)=√144=12 (см).
S=12*9=108 (cм²).
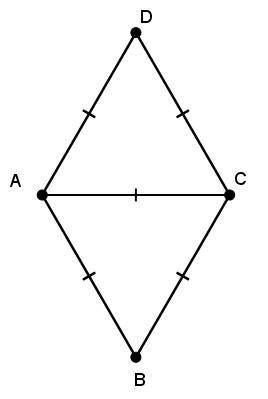
7. Пусть меньшая диагональ - х. ⇒
Большая диагональ - х+8.
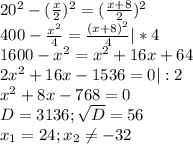
24+8=32 (см). ⇒
S=(24*32)/2=12*32=384 (cм²).
8. S=10*9,5=95 (дм²) s=0,5²=0,25 (дм²) ⇒
N=95/0,25=380 (квадратов).
1) Рассмотрим треугольник МNK:
Сумма углов в любом треугольнике = 180 градусов, тогда:
5х + 9х + 4х = 180
18х = 180
х = 10
Тогда угол MNK = 9*10 = 90 градусов.
угол NMK = 5*10 = 40 градусов.
угол MKN = 4*10 = 50 градусов.
2) Рассмотрим треугольник АВС:
Угол АСВ = 180 - 90 - 40 = 50 градусов.
tgA = BC/AB, следовательно ВС = АВ*tgA = 3*tg40
3) Треугольники АВС и MNK подобные по первому признаку. Значит:
АВ/KN = BC/NM = AC/KM = 3/9 = 1/3 (коэффициент подобия)
4) Отношение площадей подобных треугольников равно квадрату коэффициента подобия, следовательно:
Sabc / Smnk = (1/3)^2 = 1/9.
5) Отношение периметров подобных треугольников равен коэффициенту подобия, т. е.:
Pabc / Pmnk = 1/3.
Объяснение: