Объяснение:
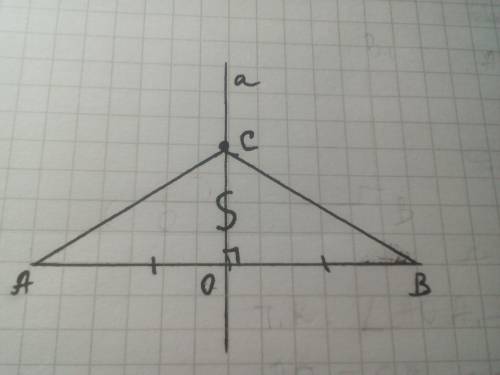
Дано: отрезок АВ, прямая а, а⊥АВ, АО=ОВ. Доказать что АС=ВС.
Возьмем на прямой а точку С, построим ΔАВС.
АО=ОВ, ∠АОС=∠ВОС=90° по условию, СО - общая сторона, значит
ΔАОС=ΔВОС и тогда АС=ВС. Доказано.
4.
Дано:
ABC - прямоугольный треугольник
AB = 5см
BC = 12см
AC - гипотенуза
BD - высота, опущенная на гипотенузу AC
Для начала вычислим длину гипотенузы AC, воспользовавшись теоремой Пифагора:
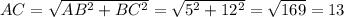
Опустив высоту AD на гипотенузу AC у нас получилось два прямоугольный треугольника - ABD с гипотенузой AB и BCD с гипотенузой BC. Пусть AD = x, тогда DC = 13 - x, так как AC = 13 см.
Поскольку высота AD является общим катетом для треугольников ABD и BCD запишем:
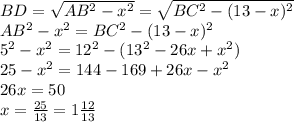
Итак, AD = x =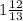 
см., а DC = 13 - x = 
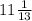см.
Найдём высоту BD:
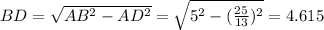см.
Высота BD делит гипотенузу AC на отрезки 1 12/13 см. и 11 1/13 см.
Высота BD равна 4,615 см.
(странные какие-то цифры, но я перепроверил решение несколько раз - всё сходится вроде бы...)
5.
Косинус угла равен отношению прилежащего катета к гипотенузе.
AB является гипотенузой. Следовательно:
cos(30) = 2 / AB
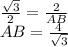
Проекция ребра SA на плоскость будет OA (SO ┴ (ABCDEF) и равна радиусу описанной около основания (здесь правильного шестиугольника) , что свою очередь равна сторону шестиугольника a₆ = R =acosα ; SO =H =asinα .
Vпир =1/3*Sосн*H =1/3*6*√3/4*(acosα)²*asinα =(√3/2)*cos²α*sinα*a³ .
При α=60° ; a= 2 получаем : Vпир = (√3/2)*1/4*(√3/2*8 =3/2.
Апофема пирамиды является образующий конуса
Vкон =1/3*π*r² *H
r = (√3/2)*R =(√3/2)*acosα.
Vкон =1/3*π*((√3/2)*acosα)*asinα =.(π/4)*cos²α*sinα*a³ .
Получилось Vкон = ( π/2√3) *Vпир .
При α=60° ; a= 2 получаем : Vкон =( π/2√3)*3/2 =π√3/6.
L =√(a² - (R/2)² =√(a² -(1/2*acosα)²) =a/2*√(4 - cos²α)
Объяснение: