Прямые АВ и CD не параллельные, то есть пересекающиеся.
Дано: угол ABC =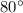 
угол BCD =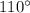 
_____________________
Д-ть АВ не параллельно CD
Решение
1) Предположим, что прямые АВ и СD параллельны. Тогда угол АВС = углу BCD = 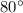(как при параллельных прямых АВ и CD и секущей BC)
2) Так как сумма углов в треугольнике равна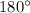 
(по теореме о сумме углов в треугольнике), мы приходим к противоречию с первым пунктом моего решения так как угол СВD и угол ВСD в сумме уже дают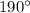 
3) Мы пришли к противоречию, значит наше предположение не верно, и значит прямая АВ не параллельна CD. Ч.т.д.
Поскольку площадь основания равна 16 см2, то сторона призмы = 4 см.
B1D - диагональ призмы, тогда BD - диагональ основы и проекция B1D на основу.
BD=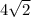
как диагональ основы, которая является квадратом.
Отсюда за теоремой Пифагора с треугоьника BB1D:
B1D=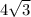
см.
Расстоянием от AA1 до B1D является перпендикуляр.
Проекция этого перпендикуляра - половина BD
Если соеденить концы этих отрезков, то получится прямоугольник. Отсюда следует, что:
MN=BD/2=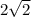
, MN - расстояние между прямыми AA1 и B1D
Объяснение:
Если BD — медиана и высота, то AD = DC, ∠ADB = ∠CDB = 90°, BD — общая. ΔABD = ΔCBD по двум катетам.
Откуда АВ = ВС, таким образом, ΔАВС — равнобедренный.