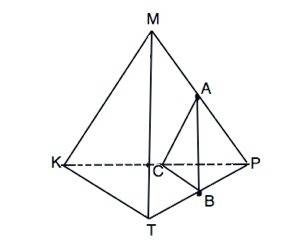
По условию секущая плоскость параллельна плоскости КМТ.
Точки А и В лежат в плоскости грани МРТ и являются серединами сторон МР и ТР треугольника МТР.
Следваоетльно, прямая АВ параллельна МТ.
Из т.В проведем прямую ВС параллельно КТ.
ВС - средняя линия ∆ КТР.
С- середина КР, АС - средняя линия ∆ МКР и параллельна МК.
Две пересекающиеся прямые АВ и МС плоскости АВС параллельны двум пересекающимся прямым МТ и ТК плоскости МКТ. Это признак параллельности плоскостей, следовательно, АВС - искомое сечение.
Треугольники АСО и ДОВ равны, так как
∠АОС=∠ДОВ как вертикальные углы,
АО=ОВ и СО=ОВ по условию.
Периметр данной фигуры равен сумме периметров двух данных равных треугольника.
Найдем периметр одного треугольника АОС.
P=6+8+10=24 см;
Периметр данной фигуры 24+24=2*24=48 см
ответ: периметр данной фигуры 48 см.