1) Известно, что у вписанного в окружность четырехугольника сумма противоположных углов равна 180 градусов. Последовательно вычитаем из 180 21 и ли 49 и находим больший угол. 2) В правильном многоугольнике углы и стороны равны. В правильном многоугольнике, вписанном в окружность углы лежат на окружности, следовательно отрезки соединяющие углы с центром окружности будут радиусы. Все проведенные радиусы к углам правильного многоугольника, деля его на равнобедренные треугольники, одновременно деля углы пополам. Следовательно углы при основании этих треугольников будут равны 70 гр. Следовательно углы при вершине этих треугольников будут равны 180-70-70=40 гр. Их общая сумма равна 360 гр. Отсюда 360:40=9 сторон.
1) Если в треугольнике ABC углы A и B равны соответственно 36 и 64 градусов, то внешний угол этого треугольника при вершине C равен 100 градусов. ДА, т.к. градусная мера внешнего угла треугольника = сумме внутренних, НЕ смежных с ним углов 36+64=100 2) Если 3 угла одного треугольника соответственно равны 3 углам другого треугольника , то такие треугольники равны. - это признак ПОДОБИЯ треугольников по трем углам НЕТ, 3) Если один из острых углов прямоугольного треугольника равен 20 градусов, то другой равен 80 градусов. Сумма углов треугольника = 180, тогда 180-90-20=80 ДА, ДА, ДА ДА
Объяснение:
Задание №1.
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
Задание №2.
Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то этот треугольник - прямоугольный.
Задание №3.
Рассмотрим четыре равных прямоугольных треугольника.
Соединим эти четыре прямоугольных треугольника.
Получим квадрат, в который вписан еще один квадрат, похожий на ромб.
Одна половина стороны квадрата равна a, другая - b. Площадь первого квадрата будет равна (a+b)^2.
Сторона второго квадрата равна с, следовательно, площадь будет равна c^2.
А площадь всего многоугольника будет равна сумме площадей треугольников и второго квадрата.
Запишем это так:
4 * 0,5 * a * b + c^2 = a^2 + 2ab + b^2
Слева получим:
2ab + c^2 = a^2 + 2ab + b^2
2ab можем уничтожить.
Останется c^2 = a^2 + b^2
Теорема доказана.
А вот что такое "Приведите пример Пифагором треугольника" я не знаю.
4. Формула Герона для нахождения площади произвольного треугольника:
S =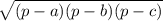
Где p - полупериметр треугольника, а все остальное - его стороны.