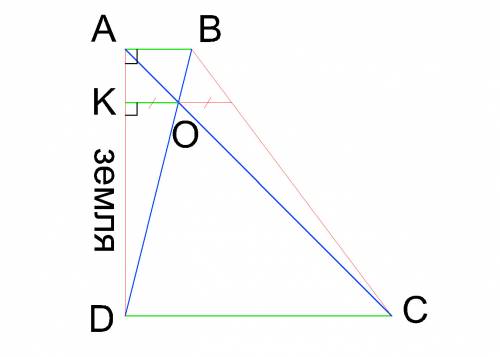
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Даны уравнения прямых: (x + 5)/4 =(y - 5)/(-3) = (z - 5)/(-5), вторая прямая задана как линия пересечения плоскостей x + 4y - z - 13 = 0
2x + 6y - z - 17 = 0.
Преобразуем уравнение второй линии.
В качестве опорной точки берём точку, лежащую в плоскости Oyz, то есть задаём значение x = 0.
4y - z - 13 = 0,
6y - z - 17 = 0.
Вычтем из второго уравнения первое: 2y - 4 = 0, y = 4/2 = 2.
z = 4y - 13 = 4*2 - 13 = -5.
Получили точку на прямой (0; 2; -5).
Теперь найдём направляющий вектор прямой как векторное произведение нормальных векторов плоскостей (это коэффициенты в уравнениях плоскостей: (1; 4; -1) и (2; 6; -1)).
i j k | i j
1 4 -1 | 1 4
2 6 -1 | 2 6 = -4i - 2j + 6k + 1j + 6i - 8k = 2i - 1j - 2k.
Нашли направляющий вектор (2; -1; -2).
Получаем каноническое уравнение прямой по точке (0; 2; -5) и направляющему вектору: (2; -1; -2).
x/2 = (y - 2)/(-1) = (z + 5)/(-2).
Преобразуем канонические уравнения прямых в параметрические:
Первая прямая (x + 5)/4 =(y - 5)/(-3) = (z - 5)/(-5)
x = 4t - 5,
y = -3t + 5,
z = -5t + 5.
Вторая прямая x/2 = (y - 2)/(-1) = (z + 5)/(-2).)
x = 2s,
y = -1s + 2,
z = -2s - 5.
Примем точку Н1 как точку пересечения первой заданной прямой и общего перпендикуляра.
Её координатам соответствует вполне конкретное значение параметра, обозначим его через to . Тогда координаты точки запишутся в виде:
x = 4to - 5,
y = -3to + 5,
z = -5to + 5.
Аналогично для точки Н2 получим:
x = 2so,
y = -1so + 2,
z = -2so - 5.
Находим вектор Н1Н2 по двум определениям.
Н1Н2 = p как результат векторного произведения направляющих векторов заданных прямых (4; -3; -5) и (2; -1; -2) (ведь он перпендикулярен обеим прямым).
i j k | i j
4 -3 -5 | 4 -3
2 -1 -2 | 2 -1 = 6i - 10j - 4k + 8j - 5i + 6k = 1i - 2j + 2k.
p = (1; -2; 2).
С другой стороны, вектор Н1Н2 проходит через 2 точки, координаты которых заданы выше.
Н1Н2: (2so - 4to + 5; -1so + 2 + 3to - 5; -2so - 5 + 5to - 5)
= (2so - 4to + 5; -1so + 3to - 3; -2so + 5to - 10).
Поскольку направляющие векторы коллинеарны, то один вектор линейно выражается через другой с некоторым коэффициентом пропорциональности «лямбда»:
(2so - 4to + 5; -1so + 3to - 3; -2so + 5to - 10) = λ(1; -2; 2).
Или покоординатно:
2so - 4to + 5 = λ*1;
-1so + 3to - 3 = λ*(-2);
-2so + 5to - 10 = λ*2.
Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными , которая стандартно разрешима, например, методом Крамера.
so to λ B
2 -4 1 -5 Определитель 9
-1 3 -2 3
-2 5 2 10
Заменяем 1-й столбец на вектор результатов B:
-5 -4 1
3 3 -2 Определитель 9
10 5 2
Заменяем 2-й столбец на вектор результатов B:
2 -5 1
-1 3 -2 Определитель 18
-2 10 2
Заменяем 3-й столбец на вектор результатов B:
2 -4 -5
-1 3 3 Определитель 9
-2 5 10
so = 9/ 9 = 1,
to = 18/ 9 = 2,
λ = 9/ 9 = 1.
Отсюда находим координаты точек.
H1: x = 4*2 - 5 = 3,
y = -3*2 + 5 = -1,
z = -5*2 + 5 = -5.
Точка Н1(3; -1; -5).
Н2: x = 2*1 = 2,
y = -1*1 + 2 = 1,
z = -2*1 - 5 = -7.
Точка Н2(2; 1; -7). Точка Н1(3; -1; -5).
Вектор Н1Н2 = (2-3=-1; 1-(-1)=2; -7-(-5)=-2) = (-1; 2; -2)
Для составления уравнения плоскости используем формулу:
nx(x - xA) + ny(y - yB) + nz(z - zC) = 0
Подставим данные и упростим выражение:
(-1) x - 3 + 2 y - (-1) + (-2) z - (-5) = 0
- x + 2y - 2z - 5 = 0