а)Даны стороны треугольника АВ и АС и угол между ними.
На произвольной прямой отложим отрезок, равный длине стороны АС, отметим на нём точки А и С.
Из вершины А заданного угла проведем полуокружность произвольного радиуса и сделаем насечки М и К на его сторонах. АМ=АК= радиусу проведенной окружности.
Из т.А на отложенном отрезке тем же раствором циркуля проведем полуокружность. Точку пересечения с АС обозначим К1.
От К1 циркулем проведем полуокружность радиусом, равным длине отрезка КМ, соединяющим стороны заданного угла.
Эта полуокружность пересечется с первой. Через точку пересечения проведем от т. А луч и отложим на нем отрезок, равный данной стороне АВ, отметим точку В. . Соединим В и С.
Искомый треугольник построен.
б) Биссектриса проводится так же, как проводится срединный перпендикуляр к отрезку.
Из точек, взятых на сторонах угла на равном расстоянии от его вершины А ( отмеряем циркулем) проводим полуокружности равного радиуса так, чтобы они пересеклись. Через точки их пересечения и А проводим луч. Треугольник АМ1К! - равнобедренный по построению, АЕ - перпендикулярен М1К1 и делит его пополам.
Треугольники АЕМ1 и АЕК1 равны по гипотенузе и общему катету. Поэтому их углы при А равны. АЕ - биссектриса.https://ru-static.z-dn.net/files/d75/da87bd0566b405886163e8b871868042.png
Объяснение:
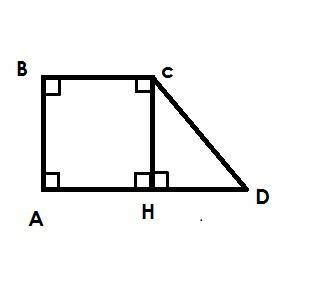
Рассмотрим ΔABC:
∠CAB = 55°; ∠ACB = 35°;
∠ABC = 180°-(∠CAB+∠ACB) = 180°-(55°+35°) = 180°-90° = 90°.
Рассмотрим ΔADC:
∠DAC = 22°; ∠ACD = 68°;
∠ADC = 180°-(∠DAC+∠ACD) = 180°-(22°+68°) = 180°-90° = 90°.
ΔABC и ΔADC прямоугольные.
В прямоугольном треугольнике медиана проведённая к гипотенузе равна её половине.M - середина AC, поэтому BM - медиана ΔABC; DM - медиана ΔADC.
2·BM = AC;
2·DM = AC;
BM = MC = MD.
В равнобедренном треугольнике углы при основании равны.ΔBMC - равнобедренный (BM=MC), BC - основание;
∠MBC = ∠BCM = 35°;
∠CMB = 180°-2·∠BCM = 180°-2·35° = 180-70° = 110°.
ΔDMC - равнобедренный (MC=MD), DC - основание;
∠MDC = ∠DCM = 68°;
∠DMC = 180°-2∠DCM = 180°-2·68° = 180°-136° = 44°.
∠DMB = ∠CMB+∠DMC = 110°+44° = 154°.
ΔDMB - равнобедренный (BM=MD), BD - основание;
∠DBM = ∠BDM = (180°-∠DMB):2 = (180°-154°):2 = 26°:2 = 13°.
ответ: 13°.