Упаралелограмі одна із сторін дорівнює 15 см , гострий кут 60 градусів і протилежна до цього кута діагональ дорівеює 21 см. знайдіть другу сторону паралелограма

👇

Ответ:

1972jkmxbr

24.11.2020

Рассм. треуг. ABD:

уголА=альфа=60 градусов, АВ=c=15 см, BD=а=21 см. По т. косинусов найдем АD=b(=х):

${a}^{2} = {b}^{2} + {c}^{2} - 2bc \cos( \alpha ) \\ {21}^{2} = {x}^{2} + {15}^{2} - 2 \times 15x \cos( 60) \\ 441 = {x}^{2} + 225 - 15x \\ {x }^{2} - 15x - 216 = 0 \\ d = {b}^{2} - 4ac = 225 + 864 = 1089 \\ x1 = \frac{15 +33 }{2} = 24 \\ x2 = \frac{15 - 33}{2} = - 9$

Корень -9 не подходит, т.к. сторона не может быть отрицательной. Получается, что вторая сторона параллелограмма равна 24 см.

ответ: 24 см.

Упаралелограмі одна із сторін дорівнює 15 см , гострий кут 60 градусів і протилежна до цього кута ді

4,5(6 оценок)

Открыть все ответы

Ответ:

Артем00796678756

24.11.2020

Треугольники АВС и АМР подобны, так как <В=<P, <C=<M (углы соответственные при параллельных прямых МР и ВС и секущих АВ и АС соответственно). Коэффициент подобия - это отношение соответственных сторон, или высот, или медиан, или периметров этих треугольников.
Значит из подобия треугольников имеем:
АО/АН = k - коэффициент подобия.
Медианы треугольника делятся в точке пересечения в отношении 2:1 считая от вершины (свойство). Значит АО/ОН=2:1. Отсюда ОН=АО:2=24:2=12см. АН=АО+ОН=36см.
Тогда АО/АН=24/36=2/3 = k (коэффициент подобия).
Из подобия треугольников АВС и АМР: МР равна ВС*k = 32*(2/3)=21и1/3.
ответ: MP=21и1/3.

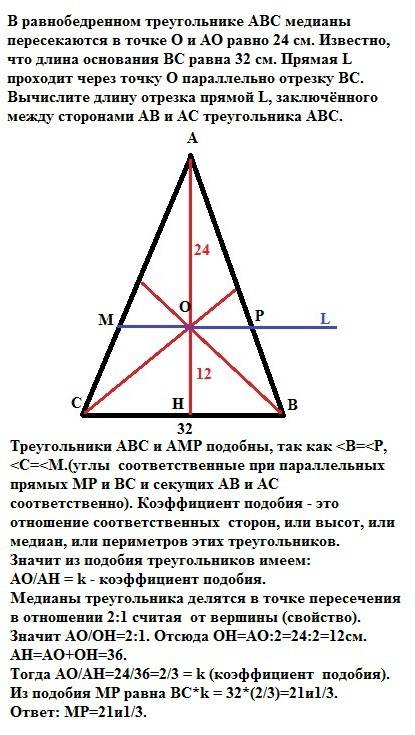
Кто-нибудь умный, ! в равнобедренном треугольнике авс медианы пересекаются в точке о и ао равно 24 с

Кто-нибудь умный, ! в равнобедренном треугольнике авс медианы пересекаются в точке о и ао равно 24 с

4,5(62 оценок)

Ответ:

Demongirl1

24.11.2020

Задача 2.

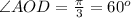
$\angle{AOD} = \frac{\pi}{3} = 60^{o}$

Задача 3.

Проекциями прямых параллельных сторонам исходного параллелограмма будут прямые, проходящие через т. пересечения диагоналей и середины сторон у параллелограмма проекции

Объяснение:

Дано

АВСД - прямоугольник

АВ = 6 см

АД = 2√3 см

Найти

уг. м/ду АС и ВД

Решение

Очевидно, что АС и ВД - диагонали прямоугольника.

Обозначим т. пересечения как т. О

Тогда уг.АОД - искомый угол между диагоналями.

Обозначим

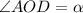
${\angle AOD} = \alpha$

По св-вам прямоугольника, его диагонали равны и в т. пересечения делятся пополам. Т.е.

АО = ОС = ВО = ОД

По Т. Пифагора можно найти диагонали:

ВД² = АВ² + АД²

BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2}

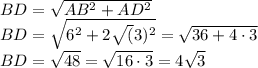
$BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2} = \sqrt{36 + 4 \cdot3} \\ BD = \sqrt{48} = \sqrt{16\cdot3} = 4 \sqrt{3}$

Соответственно

АС = ВД = 4√3

Рассмотрим тогда треугольник АОД, он равнобедренный, т.к.

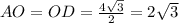
$AO = OD = \frac{4\sqrt3}{2} = 2 \sqrt{3}$

Так же 2√3 равна и сторона АД нашего прямоугольника.

То есть - мы получаем, что

АО = ОД = АД = 2√3

Следовательно - ∆АОД равносторонний,

а это означает, что искомый угол AOД

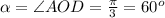
$\alpha = \angle{AOD} = \frac{\pi}{3} = 60^{o}$

Для особо дотошных:

По Т. косинусов имеем:

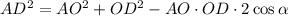
$\small {AD^2=AO^2+OD^2-AO\cdot OD \cdot 2\cos{ \alpha}}$

Отсюда

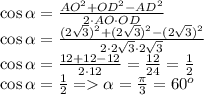
${\cos{ \alpha} = \frac {AO^2+OD^2-AD^2}{2 \cdot AO\cdot OD }} \\ {\cos{ \alpha} = \frac {(2 \sqrt{3})^2 +(2 \sqrt{3})^2 -(2 \sqrt{3})^2 }{2 \cdot 2 \sqrt{3} \cdot 2 \sqrt{3} }} \\ { \cos \alpha = \frac {12 + 12 - 12}{2 \cdot12}} = \frac{12}{24} = \frac{1}{2} \\ \cos \alpha = \frac{1}{2} = \alpha = \frac{\pi}{3} = 60^{o}$