а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен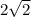 
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,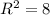 
, 
.
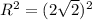
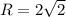в) (5; -7) - центр окружности, R²=16,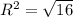 
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
Одна сторона прямоугольника равна х, х>0, вторая у, у>0. Площадь прямоугольника S = xy = 2 откуда y = 2/x. Рассмотрим функцию:
P(x)=2х+2у=2х+2*2/х=2х+4/х
Найдем производную этой функции, приравняем к нулю, получим критические точки
2-(4/х²)=0, откуда 4-2х²=0
х²≠0, х=±√2
Поскольку отрицательный корень x = -√2 не подходит по смыслу задачи, то берем критическую точку х=√2, разбиваем ею числовую ось и проверяем, какие знаки принимает производная на интервалах (0;√2);(√2;+∞)
(0)___-(√2)+
Производная функции при переходе через точку x = √2 меняет знак с минуса на плюс, поэтому х=√2 - точка минимума функции.
у=2/√2=√2
А наименьший периметр прямоугольника будет равен 4√2, если обе стороны равны √2, т.е. когда прямоугольник превратится в квадрат.