Объяснение:
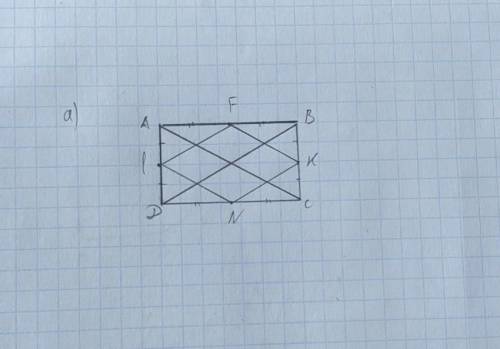
a) Ромб - параллелограмм, у которого все стороны равны, а углы непрямые.
Рассмотрим ∆DAB:
LF - средняя линия треугольника, т.к AF=FB и AL=LD => LF // DB
Рассмотрим ∆BCD:
NK - средняя линия треугольника по таким же признакам, и NK // DB => и // LF.
В ∆ABC и ∆ADC FK // AC // LN по таким же признакам.
Мы знаем, что средняя линия треугольника равна половине основания этого треугольника, и по свойствам прямоугольника: AC=DB => и FK=KN=NL=LF
=> FKNL - ромб по определению. Ч.Т.Д.
б) мы можем свободно использовать равнобедренную трапецию, у которой диагонали равны, => доказательство соответствует пункту a)
ответ: AB=BC=3√17 (см).
Объяснение: Т. к. дан равнобедренный треугольник, то:
высота, проведённая к основанию, является и медианой, и биссектрисой.⇒ BM=MC=12 (см) (т.к. AM - медиана); ∠BAM=∠CAM (т.к. AM - биссектр.).
Докажем что прямоугольные треугольники BAM и CAM равны:
→ BM=MC (т.к. BM - медиана)|
или AM - общий катет |⇒ ΔBAM=ΔCAM (по гипотенузе
→ AB=AC (по свойству) | и катету).
-----------------------------------------
→ BM=MC (т.к. BM - медиана) |
→ AM - общий катет | ⇒ ΔBAM=ΔCAM (по двум катетам).
-----------------------------------------
→ ∠B=∠C (по свойству) |
или ∠BAM=∠CAM (т.к. AM - биссектр.) |
→ BM=MC (т.к. BM - медиана) | ⇒ΔBAM=ΔCAM (по катету
или AM - общий катет | и острому углу).
------------------------------------------
→ ∠B=∠C (по свойству) |
или ∠BAM=∠CAM (т.к. AM - биссектр.) | ⇒ ΔBAM=ΔCAM (по остр.
→ AB=AC (по свойству) | углу и гипотенузе).
_____________________________________
Т.к. прямоугольные треугольники BAM и CAM равны, то чтобы найти их гипотенузу, воспользуемся теоремой Пифагора.
AB=AC=√(AM²+BM²)=√(3²+12²)=√(9+144)=√153=3√17.
-------------------------------
В формуле т.Пифагора можно было также вместо BM подставить MC. Эти стороны равны, поскольку на сторону BC опущена медиана AM.