Доказательство:
Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.
Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.
Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что, 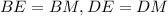 .
.
Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что 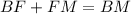 .
.
Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть 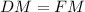 .
.
Учитывая доказанные равенства получаем,
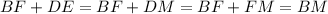
Что требовалось доказать.
Решение смотрите во вложении
По начиная от АВ=8√3см, в ΔАВС (∠С=90°) ∠А=30°, ВС=0.5 АВ=4√3/см/, тогда по теореме Пифагора
АС=√((8√3)√3)²)=√(64*3-16*3)=√(48*30=12/см/, значит, CD=16-12=4/см/
т.к. в треугольнике ВСD гипотенуза равна 8см, а против угла В, который равен 30°, лежит катет СD, то он равен половине гипотенузы ВD, т.е. 8/2=4/см/, теперь почему угол В в этом треугольнике равен 30градусов, надеюсь, понятно, потому что от 90°-60°=30°, а то, что ∠АВС =60 °, это тоже ясно, потому что ∠А смежный с внешним, равен 30°. С углами понятно, да? Осталось сказать, что в треугольнике АВD против угла А, равного 30°, лежит катет ВD, который равен 8см, поэтому гипотенуза АD равна 2*8=16/см/, на оставшуюся часть, т.е. АС приходится 16-4=12/см/ответ АС=12см; СD =4 см.
Теперь я свободен?)