Рисунки.
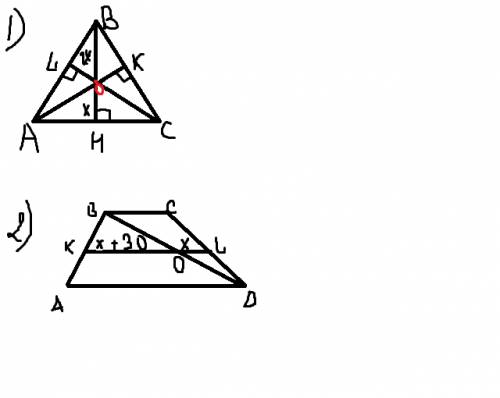
1) Дано: Треуг. АВС - равностор. Решение: Т.к. треуг. равносто-
ВН - высота ронний, то ВН=CL=AK
ВН=63 мм BH, CL, CK - высоты и бисс.
т.О- точка пересечения биссектрис В равностор. треуг. биссектр. в
Найти: ОН, ОL, ОК. точке пересечения делятся в отношении 1/2.
=> ВО=2х
ОН=х
ВО+ОН=ВН
3х=63
х=21 мм.
2) Решение: т.к. KL - сред.линия трапеции, KL=(BC+AD):2 (надо записать дробью)
=>BC=2KL-AD
Рассмотрим треуг.ABD, KO - сред. линия треуг.
=>KO=AD:2 (тоже дробь) =>AD=2KO
KO+OL=KL Пусть OL=x, тогда KO= х+30
х+30+х=110
х=40мм
AD=2KO=2*(x+30)=2*(40+30)=140мм
BC=2KL-AD=2*100-140=80мм
Найдите ∠ODC.
Диагонали прямоугольника равны и точкой пересечения делятся пополам. Значит АО = ОВ = ОС = OD.
ΔАОВ равнобедренный. ОТ - его высота, проведенная к основанию, а значит и биссектриса. Тогда
∠АОВ = 2∠ТОВ = 2 · 25° = 50°.
∠COD = ∠АОВ = 50° как вертикальные.
ΔCOD равнобедренный, значит углы при основании равны.
∠ODC = ∠OCD = (180° - 50°)/2 = 130°/2 = 65°
2. Найдите диагонали ромба, если известно, что их полусумма равна 8,2 мм и одна из них в 3 раза меньше другой.
Пусть х мм - длина одной диагонали, тогда
3х мм - длина другой.
Их сумма равна 8,2 · 2 = 16,4 мм
x + 3x = 16,4
4x = 16,4
x = 4,1
3x = 12,3
ответ: 4,1 мм, 12,3 мм
3. А₁А₂А₃А₄ - квадрат со стороной а и диагональю b. О - точка пересечения диагоналей, ОЕ - высота треугольника А₁ОА₄.
Как найти периметр треугольника А₁ОЕ?
Диагонали квадрата равны и точкой пересечения делятся пополам.
Тогда А₁О = ОА₄ = b/2.
В равнобедренном треугольнике А₁ОА₄ высота ОЕ является медианой, значит А₁Е = а/2.
ОЕ║А₁А₂ как перпендикуляры к одной прямой, О - середина А₂А₄, тогда
ОЕ - средняя линия треугольника А₁А₂А₄.
ОЕ = А₁А₂/2 = а/2
Pa₁oe = А₁О + ОЕ + А₁Е = b/2 + a/2 + a/2 = b/2 + a
4. Найдите неверное утверждение.
1) у прямоугольника диагонали не взаимно перпендикулярны;
2) и у прямоугольника, и у квадрата все стороны равны - не верно, так как у прямоугольника равны только противолежащие стороны.
3) квадрат нельзя назвать ромбом - не верно, так как ромб - это параллелограмм с равными сторонами, а у квадрата все стороны равны и противоположные стороны параллельны.
4) и у прямоугольника, и у квадрата все углы прямые.