1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒ ⇒
см
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны
То, что указанные двугранные углы равны, говорит о том, что боковые грани одинаково наклонены к плоскости основания, значит основание высоты тетраэдра лежит в центре вписанной в основание окружности. Площадь боковой поверхности пирамиды: Sб=p·l, где р - полупериметр, l - апофема боковой грани. р=(20+21+29)/2=35 см. r=S/p, где S - площадь основания. По формуле Герона S=√(p(p-a)(p-b)(p-c))=√(35(35-20)(35-21)(35-29))=210 cм². r=210/35=6 см. В треугольнике, образованном найденным радиусом, высотой пирамиды и апофемой, угол между апофемой и радиусом равен 60° (по условию). Апофема: l=r/cos60=6/0.5=12 см. Sб=35·12=420 см² - это ответ.
1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒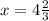 ⇒
⇒
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны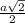
КО=МН=АВ=а
Р (КМНО=2(МН+КМ)=2a+2•(a√2/2)=a•(2+√2)