Объяснение:
Задача №1.
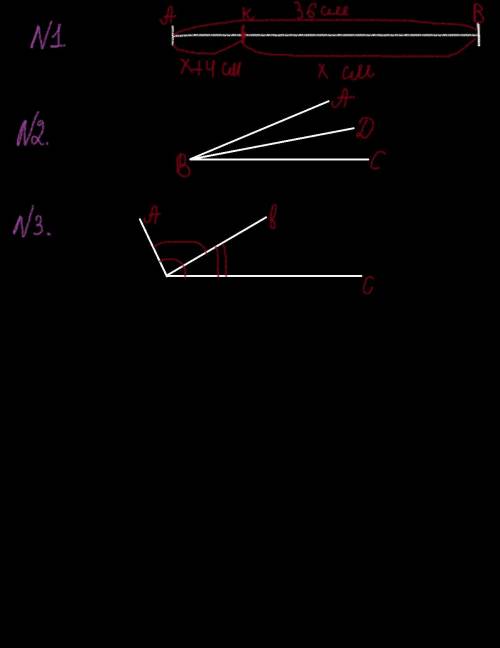
Давайте примем отрезок BK за x. Тогда отрезок AK будет равен x + 4 cм (потому что AK больше BK на 4 см).
Составляем уравнение:
x + x + 4 = 36
2x = 36 -4
2x = 32
x = 16 см - отрезок BK (потому что BK мы приняли за x).
Теперь можем найти отрезок AK. Из условия задачи известно, что AK больше BK на 4 см.
Следовательно:
AK = BK + 4 cм = 16 см + 4 см = 20 см.
Задача решена.
Задача №2.
Углы ABC и DBC являются смежными, потому что лежат на одной прямой, а две другие прямые являются дополнительными полупрямыми этих углов.
Имеем:
1) ∠ABC + ∠DBC = 180° (по свойству смежных углов)
Чтобы найти эти углы, надо составить уравнение, которое решало бы эту задачу.
Пусть x - это ∠DBC, тогда ∠ABC будет равен x + 38° (угол ABC больше ABD на 38°).
Имеем:
x + x + 38° = 180°
2x = 142
x = 71° - ∠DBC (так как угол DBC мы взяли за x).
Теперь найдем угол ABC:
2) ∠ABC = 71° + 38° = 109°
Так как эти углы делит пополам биссектриса, то углы, образованные при пересечении биссектрисы будут равны.
Чтобы их найти, мы 109 разделим на 2.
3) ∠ADB = 109° : 2 = 54,5°
Задача решена.
Задача №3.
Когда биссектриса делит угол пополам, образовываются другие углы, градусная мера которых будет в два раза меньше.
1) 150° : 2 = 75° - углы, образованные при пересечении луча b.
2) 75 + 40 = 115°
Объяснение:
Задача №1.
Давайте примем отрезок BK за x. Тогда отрезок AK будет равен x + 4 cм (потому что AK больше BK на 4 см).
Составляем уравнение:
x + x + 4 = 36
2x = 36 -4
2x = 32
x = 16 см - отрезок BK (потому что BK мы приняли за x).
Теперь можем найти отрезок AK. Из условия задачи известно, что AK больше BK на 4 см.
Следовательно:
AK = BK + 4 cм = 16 см + 4 см = 20 см.
Задача решена.
Задача №2.
Углы ABC и DBC являются смежными, потому что лежат на одной прямой, а две другие прямые являются дополнительными полупрямыми этих углов.
Имеем:
1) ∠ABC + ∠DBC = 180° (по свойству смежных углов)
Чтобы найти эти углы, надо составить уравнение, которое решало бы эту задачу.
Пусть x - это ∠DBC, тогда ∠ABC будет равен x + 38° (угол ABC больше ABD на 38°).
Имеем:
x + x + 38° = 180°
2x = 142
x = 71° - ∠DBC (так как угол DBC мы взяли за x).
Теперь найдем угол ABC:
2) ∠ABC = 71° + 38° = 109°
Так как эти углы делит пополам биссектриса, то углы, образованные при пересечении биссектрисы будут равны.
Чтобы их найти, мы 109 разделим на 2.
3) ∠ADB = 109° : 2 = 54,5°
Задача решена.
Задача №3.
Когда биссектриса делит угол пополам, образовываются другие углы, градусная мера которых будет в два раза меньше.
1) 150° : 2 = 75° - углы, образованные при пересечении луча b.
2) 75 + 40 = 115°

ответ: 1) 6 2)188,4 ( или 60π)
Объяснение:
Пусть х -внешний угол правильного многоугольника,тогда х+60° - его внутренний угол. Внешний и внутренний углы - смежные ⇒
их сумма равна 180° по свойству смежных углов, т.е.
х+х+60°=180°,
2х= 180°-60°,
х=120°:2,
х=60°,
х+60°=120°.
Сумма внутренних углов правильного многоугольника равна 180°(n-2). Решим уравнение: 120°n =180°(n-2),
120°n=180°n - 360°,
120°n -180°n= - 360°,
-60°n= - 360°
n= 6. ответ: 6
2) По свойству сторон четырёхугольника, описанного около окружности, сумма боковых сторон равнобедренной трапеции равна сумме оснований, т.е. 20+12= 32, а одна боковая сторона равна 32:2=16. Если из вершин верхнего основания опустить высоты, то они отсекут по бокам 2 треугольника, равных по гипотенузе и катету
( гипотенуза равна 16, а нижний катет равен (20-12):2=4 ).
Из теоремы Пифагора найдем высоту:
h=√(16²-4²)=√(256-16)=√240=4√15.
Значит диаметр вписанной окружности равен 4√15 и r=2√15 .
S круга =πг²= π*(2√15)²=60π=60*3,14=188,4. ответ: 188,4.