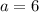 см.
см.
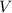 параллелепипеда =
параллелепипеда = 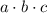 , (
, (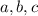 - 3 измерения параллелепипеда).
- 3 измерения параллелепипеда).
Пусть 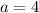 см;
см; 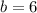 см;
см; 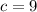 см.
см.
Тогда 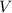 параллелепипеда =
параллелепипеда = 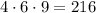 см³.
см³.
Так как 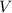 параллелепипеда =
параллелепипеда = 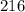 см³
см³ 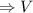 куба =
куба =
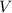 куба =
куба = 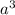 (
( - ребро куба).
- ребро куба).
![\Rightarrow a = \sqrt[3]{V}](/tpl/images/1051/8962/99108.png) куба =
куба = ![\sqrt[3]{216}](/tpl/images/1051/8962/b43dc.png) =
= 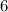 см.
см.
ответ: 9√21 (см²)
Объяснение (подробно): Нарисуем треугольник АВС. Пусть АВ=3√7, ВС=12, О- точка пересечения биссектрис из А и С.
Рассмотрим треугольник АОС. Угол ЕОС - внешний. По свойству внешнего угла сумма двух внутренних углов, не смежных с ним, равна 30°. Эти углы - половины углов при стороне АС треугольника АВС .Поэтому угол ВАС+ВСА=60°. Из суммы углов треугольника угол АВС=180°-60°=120°.
Одна из формул площади треугольника S=0,5•a•b•sinα, где а и b - стороны, α – угол между ними. S (ABC)=0,5•3√7•12•√3/2=9√21 (см²)
=========
Задача решена по данному в вопросе условию. Возможно, условие дано с ошибкой и одна из сторон не 3√7, а 7√3. Тогда площадь будет иной. Вычислите ее самостоятельно.

Объяснение:
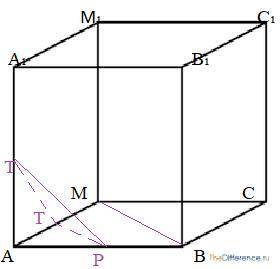
2) АВСМА₁В₁С₁ М₁-куб, Р,Т,К –середины сторон соответственно АВ, АА₁, АМ, S(сеч)= √10/4 .
Обозначим ребро куба х.
В сечении куба плоскостью, проходящей через середины сторон трех измерений-получился равносторонний ΔТКР (ΔТАР=ΔТАК=ΔКАР как прямоугольные по 2-м катетам) , S( равностор.тр)=(а²√3)/4 ⇒
√10/4=(ТР²√3)/4 , ТР²=√(10/3) .
Т.к. АВ=х, то АР=АТ=(х/2)
ΔТАР -прямоугольный по т. Пифагора (х/2)² +(х/2)² =ТР² ,
2*(х/2)² =√(10/3) , х²=2*√(10/3), х=√(40/3),
V(куба) =√(40/3)* √(40/3)* √(40/3) =40/3*√(40/3) (см³)
6 см.
Объяснение:
Объем прямоугольного параллелепипеда определяется по формуле :
По условию a= 4 см, b= 6 см, c =9 см.
Тогда объем
Объем куба определяется по формуле:
Тогда
Значит ребро куба равно 6 см.