Можно рисунок к , ! параллельно оси цилиндра на расстоянии 4 см от нее проведено сечение, пересекающее основание по хорде длиной 6 см. диагональ сечения равна 10 см. найдите объем цилиндра
Удаленное решение пользователя TwilightStar2016 верное, за исключением досадной описки в конце. Вот оно: Решение. 1)MN-касат. OE-r-следовательно <MEK=90º=>KE-высота, медиана, биссектриса. КЕ-медиана=>МЕ=ЕN=20:2=10 2)OD-r MK-касат=><KDO=90º 3)Рассмотрим треу. MEK и DOK. <MEK-общий, <KDO=<MEK=>треу. MEK ~ DOK.(по двум углам) 4)MN и MK-касат.,MD-10=>ME=MD (по двум касат.) DK=MK-MD=26-10=16см. 5) треу. MKE-прямоуг. MK^2=ME^2+EK^2(теорема Пифагора. ) EK=корень ME^2-MK^2=корень из 676-100=корень из 576=24. 6)Отношение. 10/OD=24/16=26/OK 24/16=26/OK 24×OK=16×26 24OK=416 OK=416:21 OK=17целых1/3 OE=EK-OK=24-17целых1/3=6целых2/3 (а не 6и1/3, как было в ответе). Можно было решить так: По формуле радиуса вписанной в треугольник окружности: r=S/p, где S - площадь, а "р" - полупериметр треугольника. У нас р=(26+26+20):2 = 36. S=√[p(p-a)((p-b)(p-c)] - формула Герона. S=√(36*18*18*16)=240. r=240/36=6и2/3. ответ: r=6и2/3.
Задача 6
В ΔАВС , АВ=ВС, АЕ -биссектриса, Е∈ВС. Найти Р( АВС), если ВС-АС=8 и ВЕ:ЕС=3:2.
Решение.
Пусть одна часть х. Тогда ВЕ=3х, ЕС=2х ⇒ ВС=5х ⇒ АВ=5х , т.к треугольник равнобедренный.
По т. о биссектрисе треугольника
, тогда 
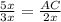⇒ AC=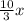
.
По условию ВС-АС=8 , поэтому 5х-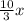
= 8 или 
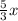=8 или х=4,8.
ВС=5*4,8=24 , АВ=24 , АС=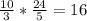
.
Р=24+24+16=64.
Задача 8
Стороны треугольника относятся как 2:3:3 . Найти периметр треугольника , если основание на 5 единиц меньше боковой стороны.
Решение .
Дан ΔАВС. АВ=ВС . Пусть одна часть х. Тогда АВ=ВС=3х, АС=2х .
По условию АС меньше АВ на 5, т.е АВ-АС=5.
Получим 3х-2х=5 или х=5 . Тогда АВ=ВС=3*5=15, АС=2*5=10 .
Р=15+15+10=40.
Задача 9
Угол при вершине равнобедренного треугольника равен 120°. , высота , опущенная на основание, равна 6 .Найти периметр треугольника .
Решение .
Дан ΔАВС , АВ=ВС ,ВН⊥АС , ∠АВС=120°.
1) Высота равнобедренного треугольника является биссектрисой ⇒∠АВН=60° .
2) ΔАВН -прямоугольный , по свойству углов ∠А=90°-60°=30°.
Против угла в 30° , лежит катет равный половине гипотенузы , т.е ВН=1/2*АВ ⇒ АВ=12 ⇒ВС=12, т.к треугольник равнобедренный.
По т. Пифагора АН²=АВ²-ВН² или АН²=12²-6² или АН=√18*6=6√3.
3) Высота равнобедренного ΔАВС является медианой, значит АН=НС=6√3 ⇒АС =12√3.
4)Р=12√3+12+12=24+12√3.