6 см.кв.
Объяснение:
Площадь прямоугольного треугольника равна половине произведения катетов
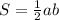
а=4 см
b=?
с=5 см
чтобы найти второй катет воспользуемся теоремой Пифагора
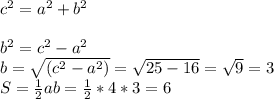
Условие задачи не совсем полное. Должно быть так:
∠2 = 50°, ∠1 = 130°, ∠4 на 42° меньше, чем ∠3.
Найдите: ∠3, ∠4, ∠5.
∠6 = 180° - ∠1 по свойству смежных углов,
∠6 = 180° - 130° = 50°.
∠6 = ∠2 = 50°, а эти углы - соответственные при пересечении прямых а и b секущей с, значит
а║b.
∠7 = ∠3 как вертикальные, а угол 4 на 42° меньше, чем угол 3 по условию, значит и
∠7 - ∠4 = 42°
Пусть ∠4 = х, тогда ∠7 = х + 42°.
∠4 + ∠7 = 180° так как это односторонние углы при пересечении параллельных прямых а и b секущей d.
x + x + 42° = 180°
2x = 180° - 42°
x = 138°
x = 69°
∠4 = 69°, ∠3 = ∠7 = 69° + 42° = 111°
∠5 = ∠7 = 111° как соответственные при пересечении параллельных прямых а и b секущей d.
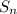= 180°·(n-2), где n-число сторон многоугольника. Получим уравнение:
S=6 см²
Пошаговое объяснение:
Площадь прямоугольного треугольника
S= 1/2 a*b, где
a и b - катеты треугольника
По условию :
а= 4 см
с=5 см
b-? см
Найдем второй катет.
По теореме Пифагора :
с²=а²+b²
b²=c²-a²
b=√c²-b²
b=√5²-4²=√25-16=√9=3 cм
Теперь найдем площадь треугольника
S= 1/2*4*3=6 cм²