Геометрия: Умоляю решите 131-134 номера.сколько сможете. 100

Умоляю решите 131-134 номера.сколько сможете. 100

👇

Увидеть ответ

Ответ:

ВиГуки247

16.03.2021

131.

1) а) Пусть x - первый угол, тогда 5x - второй угол. Сумма односторонних углов равна 180°, поэтому составим уравнение:

x + 5x = 180°

6x = 180°

x = 30° - первый угол

5 * 30° = 150° - второй угол

б) Аналогично. x - один угол, 8x - второй угол. Уравнение:

x + 8x = 180°

9x = 180°

x = 20° - первый угол

8 * 20° = 160° - второй угол

2) а) x - один угол, x + 50° - второй угол. Уравнение:

x + x + 50° = 180°

2x = 130°

x = 65° - первый угол

65° + 50° = 115° - второй угол

б) x - первый угол, x + 70° - второй угол. Уравнение:

x + x + 70° = 180°

2x = 110°

x = 55° - первый угол

55° + 70° = 125° - второй угол

132.

1) ∠CBD и ∠ADB; ∠DBA и ∠BDC

2) ∠DAB и ∠ABD

3) а) ∠BCD = 47°; б) ∠BDA = 38°

133.

1) ∠MDA; AB

2) ∠DEC; BC

3) ∠BDE; AB

134.

а) ∠BDE = 48°; ∠ADE = 132°

б) ∠BED = 75°; ∠CEK = 75°

4,5(3 оценок)

Открыть все ответы

Ответ:

LeraBelenko

16.03.2021

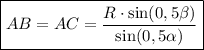
$\boxed{AB = AC = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}}$

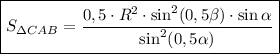
$\boxed{S_{зCAB} = \dfrac{0,5 \cdot R^{2} \cdot \sin^{2} (0,5\beta) \cdot\sin \alpha }{\sin^{2} (0,5\alpha )}}$

Объяснение:

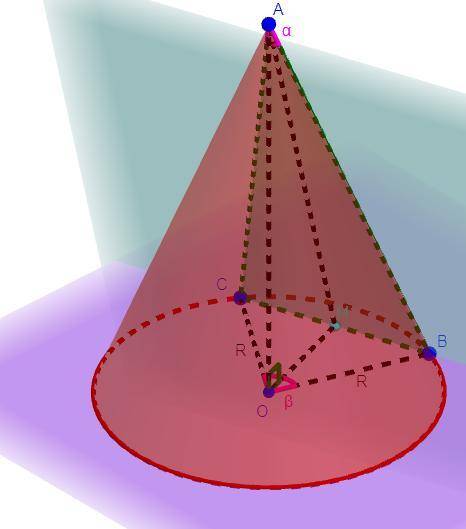
Дано: OC = OB = R, ∠BOC = β, ∠BAC = α, O - центр окружности в основании конуса

Найти: AC,BC, 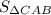$S_{зCAB}$ - ?

Решение: Пусть точка M - середина отрезка CB. Рассмотрим треугольник ΔCOB. Треугольник ΔCOB - равнобедренный, так как по условию OC = OB = R. Проведем отрезок OM. Так как по построению CM = MB, то по определению MO - медиана равнобедренного треугольника ΔCOB. Так как CB - основание треугольника ΔCOB

(по условию OC = OB = R), то по теореме медиана проведенная к основания равнобедренного треугольника является биссектрисой и высотой, тогда ∠COM = ∠BOM = ∠BOC : 2 = β : 2 = 0,5β. Так как OM - высота, то треугольник ΔMOB - прямоугольный. Рассмотрим треугольник ΔMOB. 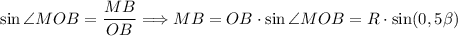$\sin \angle MOB = \dfrac{MB}{OB} \Longrightarrow MB = OB \cdot \sin \angle MOB = R \cdot \sin (0,5\beta )$ .

Рассмотрим треугольник ΔCAB. Треугольник ΔCAB - равнобедренный, так как по условию AC = AB как образующие конуса. Проведем отрезок AM. Так как по построению CM = MB, то по определению MA - медиана равнобедренного треугольника ΔCAB. Так как CB - основание треугольника ΔCAB (AC = AB как образующие конуса), то по теореме медиана проведенная к основания равнобедренного треугольника является биссектрисой и высотой, тогда

∠CAM = ∠BAM = ∠BAC : 2 = α : 2 = 0,5α. Так как AM - высота, то треугольник ΔMAB - прямоугольный. Рассмотрим треугольник ΔMAB.

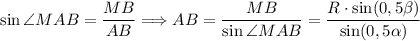$\sin \angle MAB = \dfrac{MB}{AB} \Longrightarrow AB = \dfrac{MB}{\sin \angle MAB} = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}$ .

Так как AC = AB как образующие, то 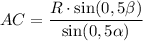$AC = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}$ .

По формуле площади для треугольника ΔBAC:

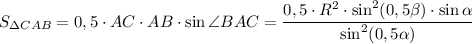$S_{зCAB} = 0,5 \cdot AC \cdot AB \cdot \sin \angle BAC = \dfrac{0,5 \cdot R^{2} \cdot \sin^{2} (0,5\beta) \cdot\sin \alpha }{\sin^{2} (0,5\alpha )}$ .

Через две образующих конуса, угол между которыми равен α, проведена плоскость, пересекающая основани

4,4(18 оценок)

Ответ:

Ania07

16.03.2021

Задача 3.
В равнобедренном треугольнике (ACD, так как AD=CD) медиана (BD, так как делит сторону пополам (AB=BC)) проведённая к основанию (AC) является высотой и биссектрисой. Высота образует перпендикуляр, то есть прямой угол. Значит, ∠ABD=∠CBD=90°.
Так как треугольник ADC равнобедренный ∠C=∠A=35°
ответ: ∠А=35°, ∠ABD=90°.
Задача 4.
Вообще нерешаемая задача, не может быть такого, что в треугольнике сумма углов больше 180°, но скорее всего задача на то же правило, что следует из равенства углов А и В. Вероятно, АК=КВ=2см. Только так.