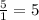Равнобедренный треугольник условно назовём ABC с основанием AC. Если периметр треугольника ABC равен 24 см, то значит, что каждая его сторона будет равна по P = 24 : 3 = 8 см (т.к. у равнобедренного треугольника все стороны равны). Равнобедренный треугольник начертим от стороны BC. Получится равнобедренный треугольник BCD с основанием BC. Мы знаем, его его периметр равен 36 см. У треугольника BCD равны стороны BD и DC, а сторону BC мы знаем. Значит, сначала находим сумму длин равных сторон 36 - 8 = 28 см. Значит, BD = DC = 28 : 2 = 14 см ответ: BC = 8 см, BD = 14 см, DC = 14 см
Тр-ник АВС - равнобедр. АС - основание. О - точка внутри тр-ка.Через точку О проведем две прямые, параллельные бокавым сторонам АВ и ВС. Эти прямые пересекут основание АС в точках М и К. Значит ОМ параллельно АВ, ОК параллельно ВС. Мы имеем две параллельные прямые АВ и МО и секущую АС. Угол ВАС = ОМК как соответствующие углы при указанных параллельных прямых и секущей. Аналогично, паралельные прямые ВС и ОК и секущая АС. Углы ВСА = ОКМ как соответствующие при указанных параллельных прямых и секущей. В тр-ке МОК два угла при основании МК равны двум углам тр-ка АВС при основании АС. Тр-ник, у которого два угла равны, называется равнобедренным. Доказано.
Тангенс и котангенс взаимно обратные, поэтому:
а) tgA=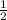
b)tgA=