ответ:2.5.3 в прямоугольном треугольнике cosA = sinB или cosB=sinA. у нас есть Cos A 173/371. значит sinB будет 173/371
2.5.4 Синус - отношение противолежащего катета к гипотенузе. То получаем, что катет BC=4√11, а гипотенуза = 15; По т. Пифагора найдем катет AC= √225-176=7
то sinB=7/15
2.5.5 Косинус-отношение прилежащего катета на гипотенузу, косинус угла А равен √91\10, значит прилежащий катет, т.е АС=√91, а гипотенуза=10.
По теореме Пифагора находим катет ВС:
ВС²=ВА²-СА²
ВС²=100-91=9
ВС=3
Косинус-отношение прилежащего катета на гипотенузу, значит косинусом угла В будет служить отношение ВС\ВА=3\10
ответ: 0,3
2.5.6 tg A = sin A/ cos A
Применим основное тригонометрическое тождество:
sin A=√(1-cos²A)=√(1-(√2/4)²)= √(1-2/16)=√(1-1/8)=√(7/8)
Тогда tg A = √(7/8):(√2/4)= √(7/8)·4/√2=4·√(7/16)=4·¼·√7=√7.
ответ: √7.
2.5.7 sina=3(√10)/(√10)²=3/√10
cosa=√(1-sin²x)=√(1-9/10)=√(1/10)=1/√10
tga=sina/cosa=(3/√10)/(1/√10)=(3/√10)*√10=3
 ед².
ед².
Объяснение:Обозначим данную пирамиду буквами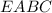 .
.
Проведём высоту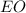 . Точка
. Точка 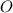 - центр
- центр 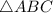 - точка пересечения, медиан, высот и биссектрис треугольника.
- точка пересечения, медиан, высот и биссектрис треугольника.
Проведём апофему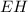 (апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне
(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 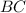 основания пирамиды.
основания пирамиды.
Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.
Проведём высоту в
в 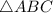 .
.
Т.к.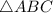 - равносторонний ⇒
- равносторонний ⇒  - высота, медиана, биссектриса.
- высота, медиана, биссектриса.
Высота и апофема
и апофема 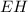 имеют общее основание, а именно точку
имеют общее основание, а именно точку 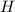 , т.к.
, т.к.  - медиана, а апофема
- медиана, а апофема 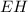 делит
делит 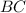 пополам (по свойству).
пополам (по свойству).
Рассмотрим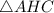 :
:
Найдём высоту по теореме Пифагора:
по теореме Пифагора: 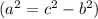
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.
Рассмотрим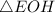 :
:
Если угол прямоугольного треугольника равен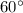 , то напротив лежащий катет равен произведению меньшего катета на
, то напротив лежащий катет равен произведению меньшего катета на 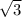 .
.
Найдём апофему по теореме Пифагора: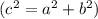
====================================================
⇒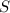 бок. поверх. =
бок. поверх. = 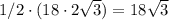 ед².
ед².
⇒ полн. поверх. =
полн. поверх. =  ед².
ед².