Секущая состоит из внешней (вне окружности) и внутренней (хорде) части. Наибольшая секущая проходит через центр окружности и содержит диаметр, – все остальные секущие будут меньше, так как любая хорда меньше диаметра
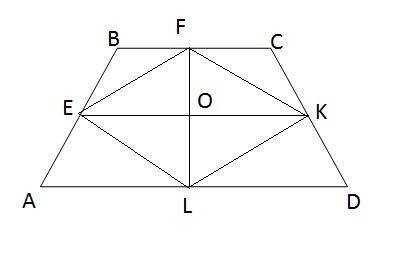
Обозначим А точку, из которой проведены касательная и секущая, В - точку касания, О - центр окружности, АС - секущую, М - её пересечение с окружностью.
Задачу можно решить по т.Пифагора или по свойству касательной и секущей.
1) Соединим О и В.
В ∆ АОВ катет АВ=24 - касательная, катет ВО=R - радиус, гипотенуза АО - секущая без радиуса СO=32-R/
По т.Пифагора
ВО²=АО*-АВ²
R²=(32-R)²-24*
R*=1024-64R+R²-576
64R=448 ⇒R=7
S=πR²=49π см²
* * *
2) Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.(теорема).
АС•AM=АВ²
АМ=АС-2R
Тогда
32•(32-2R)=576
Решив уравнение, получим R=7 и площадь круга 49π см²
Пусть D - начало координат
Ось X - DA
Ось У -DC
Ось Z -:DD1
Вектора
В1D ( -6;-6;-6 )
BB1 (0;0;6)
DC (0;6;0)
Искомые расстояния
| В: В1D | = | ВВ1 х В1D | / | В1D | =
√ (36^2+36^2) / √ (36+36+36)= 2 √6
| C; B1D | = | DC x B1D | / | B1D | = √ (36^2+36^2) / √ (36+36+36) = 2 √6