Заметим, что BEFA -- вписанный четырёхугольник, так как углы, опирающиеся на сторону АВ равны. Отсюда имеем равенство углов AEF, ABF и EAF, EBF. Значит,
Аналогично угол FEC равен углу BAC. Значит, в треугольниках ACB и ECF все углы равны и они подобны
Вписанный треугольник АВС в окружность с центром О. Градусная мера всей окружности 360°. Найдем градусные меры трех дуг, для этого обозначим одну часть через х, получится уравнение: х+2х+3х=360 х=360/6=60° Получается градусная мера дуги АВ=60°, дуги ВС=120°, дуги АС= 180°. Углы АВС, ВСА и САВ являются вписанными углами (вершины их лежат на окружности, а обе стороны пересекают эту окружность). Градусная мера вписанного угла равна половине дуги, на которую он опирается. <АВС =180/2=90°, <ВСА =60/2=30° и <САВ =120/2=60°. Исходя из того, что <АВС =90°, делаем вывод, что ΔАВС - прямоугольный и гипотенуза АС является диаметром окружности (вписанный угол, опирающийся на диаметр - прямой). Напротив меньшей стороны лежит меньший угол, значит катет АВ=17. Катет, лежащий против угла 30°, равен половине гипотенузы, следовательно радиус окружности ОА=ОВ=ОС=АВ=17 ответ: 17
Объяснение:
Заметим, что BEFA -- вписанный четырёхугольник, так как углы, опирающиеся на сторону АВ равны. Отсюда имеем равенство углов AEF, ABF и EAF, EBF. Значит,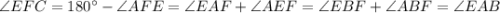
Аналогично угол FEC равен углу BAC. Значит, в треугольниках ACB и ECF все углы равны и они подобны