Объяснение:
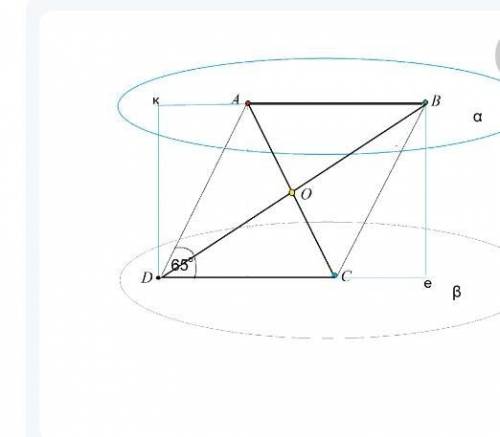
Точки А и В лежат в плоскости альфа, а точки С и D- в плоскости бета, причём альфа параллельна бета, АВ=СД, а отрезки АС и ВD пересекаются.
а) докажите, что АВ параллельна СD.
б) Один из углов четырёхугольника АВСD равен 65 градусов. Найдите остальные углы
а) АС и ВD пересекаются.
Через две пересекающиеся прямые можно провести плоскость, и притом только одну; то же справедливо и для параллельных прямых.
Следовательно, прямые АВ и СD лежат в той же плоскости. что АС и ВD.
Проведем из D и В перпендикуляры кD и Ве к противоположной плоскости.
Т.к. плоскости α и β параллельны, то кD и Ве параллельны и равны ( на основании того, что это - перпендикуляры между параллельными плоскостями)
Прямые кВ и Dе лежат в одной плоскости кВeD, расстояние между ними равно, следовательно, они параллельны.
АВ принадлежит кВ, DС принадлежит Де, следовательно, АВ||СD.
б) Четырехугольник, в котором противоположные стороны равны и параллельны, - параллелограмм.
Противоположные углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°
Острые углы четырехугольника АВСD равны по 65°. Тупые по-180-65=115°———
2. Откладываете на этой прямой отрезок АВ (замерив данный Вам катет циркулем), равный данному катету.
3. От точки А на этой же прямой откладываете отрезок АА1, равный данному катету, но в противоположную сторону.
4. Из точек А и В циркулем проводите дуги радиусом, БОЛЬШИМ АА1 и получаете точку пересечения этих дуг М.
5. Соединяете точки А и М прямой - это будет перпендикуляр к прямой в точку А, то есть перпендикуляр, содержащий второй катет.
6. Теперь от точки В строите данный Вам острый угол. Для этого на данном нам угле радиусом R проводим окружность и получаем точки Р и К. Этим же радиусом проводим окружность с центром в точке В на прямой "а". Получаем точку Р1. Замеряем циркулем расстояние РК на данном нам угле. Это радиус r. Из точки Р1 (как центр) на прямой "а" радиусом r проводим окружность и в точке пересечения двух окружностей получаем точку К1. Через точки В и К1 проводим прямую "b". Получили данный нам угол В.
7. Пересечение прямой b с перпендикуляром и даст Вам третью точку С искомого треугольника.
Получили искомый треугольник АВС.