Пусть дана равнобедренная трапеция с диагоналями см и см — медиана (см. вложение).
Сделаем дополнительное построение: проведем прямую . Образовался равнобедренный треугольник с боковыми сторонами см, равновеликий с трапецией (так как треугольники и равны по третьему признаку равенства треугольников). Следовательно, средние линии и тоже равны (средние линии и соответственно равны треугольникам и ).
Рассмотрим равнобедренный треугольник . Так как см — его средняя линия, то см. Опустим перпендикуляр — высота, биссектриса и медиана. Значит, см.
Рассмотрим прямоугольный треугольник
По теореме Пифагора: см.
Следовательно, площадь треугольника составляет см².
Так как треугольник и трапеция равновеликие, то площадь трапеции равна 48 см².
Пусть АВСД - трапеция, у которой углы В и С - прямые (АВ - большее основание, СД - меньшее основание) . Проведем из тупого угла Д высоту на основание АВ (получим точку Е) , а из центра вписанной окружности - перпендикуляры (радиусы) на сторону АД и основание СД. Получим точку М (на основании СД) и точку N - на стороне АД. МД=NД = 4. Тогда АЕ = (АВ+R - СД-R) = 25-4=21. Из прямоугольного треугольника АДЕ по теореме Пифагора находим высоту трапеции: = (29^2-21^2)^(1/2)=20. Одновременно это и диаметр вписанной окружности. Тогда СД =СМ+МД= 10+4=14, АВ=10+25=35. Площадь трапеции: (14+35)*20/2=490.
Пусть одна часть высоты = 2а, другая = 5а, тогда вся высота 7а. Меньший отрезок - радиус вписанной окружности, r=2a. Свяжем стороны через площадь: С одной стороны, S=bh/2, где b - основание, h - высота; С другой - S=p*r, где p - половина периметра, r - радиус вписанной окружности, следовательно bh/2=pr; b*7a/2=28*2a b=16 (см) - основание треугольника. Вписанная окружность делит основание на 2 равных отрезка касательных. Тогда, боковая сторона разделится на два отрезка касательных - один из них будет равен половине основания, другой нужно найти; следовательно, y+y+y+y+x+x=56 4y+2x=56 x+2y=28; y=8 x=28-16=12 (см), значит, боковые стороны = 12+8=20 (см). ответ: 16 см; 20 см; 20 см.
Пусть дана равнобедренная трапеция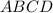 с диагоналями
с диагоналями 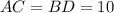 см и
см и 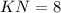 см — медиана (см. вложение).
см — медиана (см. вложение).
Сделаем дополнительное построение: проведем прямую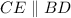 . Образовался равнобедренный треугольник
. Образовался равнобедренный треугольник 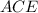 с боковыми сторонами
с боковыми сторонами 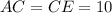 см, равновеликий с трапецией
см, равновеликий с трапецией 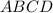 (так как треугольники
(так как треугольники 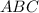 и
и 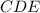 равны по третьему признаку равенства треугольников). Следовательно, средние линии
равны по третьему признаку равенства треугольников). Следовательно, средние линии 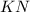 и
и 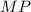 тоже равны (средние линии
тоже равны (средние линии 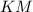 и
и 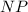 соответственно равны треугольникам
соответственно равны треугольникам 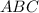 и
и 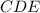 ).
).
Рассмотрим равнобедренный треугольник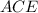 . Так как
. Так как 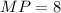 см — его средняя линия, то
см — его средняя линия, то 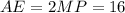 см. Опустим перпендикуляр
см. Опустим перпендикуляр 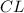 — высота, биссектриса и медиана. Значит,
— высота, биссектриса и медиана. Значит, 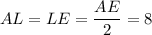 см.
см.
Рассмотрим прямоугольный треугольник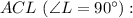
По теореме Пифагора: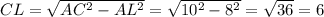 см.
см.
Следовательно, площадь треугольника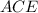 составляет
составляет 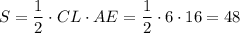 см².
см².
Так как треугольник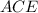 и трапеция
и трапеция 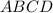 равновеликие, то площадь трапеции равна 48 см².
равновеликие, то площадь трапеции равна 48 см².
ответ: 48 см².