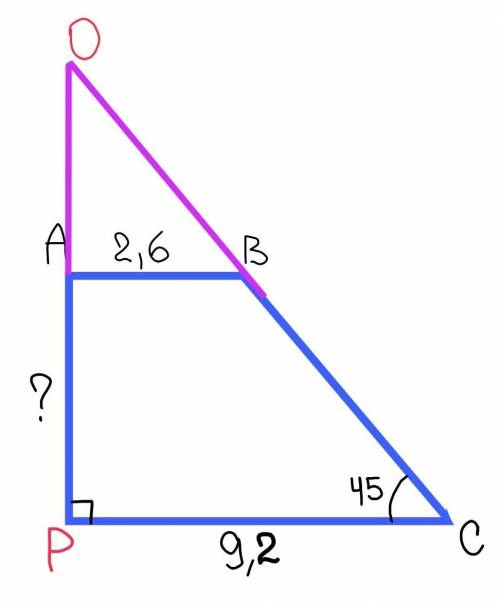
Продлим РА за точку А и СВ за точку В, точку пересечения назовём О.
∆РОС – прямоугольный с прямым углом Р.
Сумма острых углов прямоугольного треугольника равна 90°. Исходя из этого: угол РОС=90°–угол ОСР=90°–45°=45°.
Получим что угол РОС=угол ОСР, тогда ∆РОС – равнобедренный с основанием ОВ.
Тогда РО=РС=9,2 см.
Основания трапеции параллельны, тоесть АВ//РС.
Следовательно: угол ОВА=угол ОСР как соответственные при параллельных прямых АВ и РС и секущей ОС; тогда угол ОВА=45°.
Угол АОВ=45° (доказано ранее)
Получим что угол ОВА=угол АОВ.
Тогда ∆АОВ – равнобедренный с основанием ОВ. Следовательно АО=АВ=2,6 см.
РА=РО–АО=9,2–2,6=6,6 см.
ответ: 6,6 см.
Совместим их так, чтобы луч ВА совпал с лучом DC, а луч ВС совпал с лучом DA.
Так как у прямоугольника противоположные стороны равны, то совпадут и отрезки АВ и СD, и ВС и AD.
Тогда совпадут и третьи стороны треугольников.
Треугольники совпали при наложении, значит они равны.
2) АВ = CD и ВС = AD как противоположные стороны прямоугольника,
∠АВС = ADC = 90°, ⇒
ΔАВС = ΔCDA по двум сторонам и углу между ними ( по первому признаку)
АС - общая сторона треугольников АВС и ADC,
∠ВАС = ∠DCA как накрест лежащие при пересечении АВ║CD секущей АС,
∠ВСА = ∠DAC как накрест лежащие при пересечении ВС║AD секущей АС, ⇒ ΔАВС = ΔCDA по стороне и двум прилежащим к ней углам ( по второму признаку)