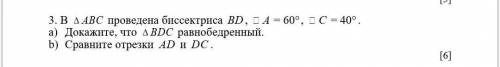
ответ: В соответствии с классическим определением, уго� между векторами, отложенными от одной точки, определяется как кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. Для заданного варианта углы между векторами могут быть определены из соотношения углов в треугольнике ABC, в котором ∠АСВ=90°, ∠СВА=40°, соответственно ∠САВ=180°-(90°+40°)=50°. Тогда -
- угол между векторами СА и СВ равен ∠АСВ=90°;
- угол между векторами ВА и СА равен ∠САВ=50°;
- угол между векторами СВ и ВА равен ∠САВ+∠АСВ=50°+90°=140°
Подробнее - на -
Объяснение:
∠В = 180°-60°-40°=80°
ВД - биссектриса, следовательно ∠ДВс=∠АВД = 40°.
Треугольник равнобедренные, когда два его угла равны. Угол ДВС = углу С, следовательно ΔДВС - равнобедренный.
Сторона ДС = стороне ВД. Против большего угла лежит большая сторона, а против меньшего - меньшая. ВД лежит напротив ∠А, а АД против ∠АВД. ∠АВД больше ∠А, ⇒ ВД больше АД ⇒ ДС больше АД
Объяснение: