Нарисуем этот треугольник.
Обозначим точки буквами- см.рисунок.
Получились прямоугольные треугольники, высоты в который определяются по формуле высоты равностороннего треугольника
h=(а√3):2
Найдем сторону ВК в треугольнике КВМ
3=(ВК√3):2
(ВК√3)=3*2=6
ВК=6:√3=2√3
По той же формуле найдем АВ
5=(АВ√3):2
АВ√3=5*2=10
АВ=10:√3=(10√3):3
АК=(10√3):3 -2√3=(10√3 -6√3):3=(4√3):3
КН=√3(4√3):3):2=12:6=2см
рисунок - во вложении
----------------------------------------------
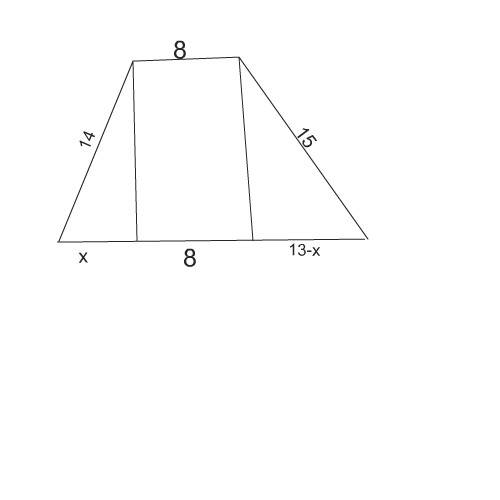
Рисуем трапецию.
Опустим из ее углов при меньшем основании высоты на нижнее основание.
Получили один прямоугольник и два прямоугольных треугольника при боковых сторонах как гипотенузах.
Найдем значение высот и приравняем их.
Для этого отрезок основания при боковой стороне 14 обозначим х, а отреок ( катет) при боковой стороне 15 будет 21-х-8=13-х
14²-х²=15²-(13-х)²
Из этого уравнения найти х, затем из прямоугоьного треугольника с гипотенузой 14 и катетом, равным найденному х, вычислить высоту трапеции.
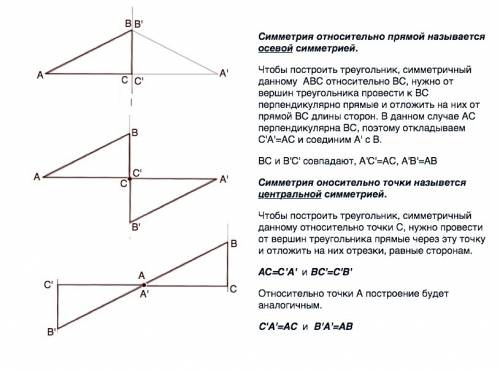
Симметрия относительно прямой называется осевой симметрией.
Чтобы построить треугольник, симметричный данному АВС относительно ВС, нужно от вершин треугольника провести к ВС перпендикулярно прямые и отложить на них от прямой ВС длины сторон. В данном случае АС перпендикулярна ВС, поэтому откладываем С'A'=AC и соединим A' c В.
ВС и В'C' совпадают, А'C'=AC, A'B'=АВ
Симметрия оносительно точки назывется центральной симметрией.
Чтобы построить треугольник, симметричный данному относительно точки C, нужно провести от вершин треугольника прямые через эту точку и отложить на них отрезки, равные сторонам.
АС=С'A'
BC'=C'B'
Относительно точки А построение будет аналогичным.
C'A'=AC
B'A'=AB
По теореме косинусов