ответ:В треугольной пирамиде проекция бокового ребра L на основание совпадает с отрезком, равным (2/3) высоты h треугольника в основании пирамиды.
h =(3/2)* (L*cos 60°) = (3/2)*(√3*(1/2)) = 3√3/4.
Сторона а основания равна:
а = h/cos 30° = (3√3/4)/(√3/2) = 3/2.
Высота пирамиды H = L*sin 60° = √3*(√3/2) = 3/2.
Основание пирамиды вписывается в шар по окружности радиуса Ro.
Ro = (1/3)h/(sin 30°) = (1/3)*(3√3/4)/(1/2) = √3/2.
Теперь переходим к рассмотрению осевого сечения пирамиды через два боковых ребра, развёрнутых в одну плоскость.
Для шара это будет диаметральное сечение.
Радиус шара Rш = (abc)/(4S).
Здесь a и b - боковые рёбра, с - диаметр описанной около основания пирамиды окружности (с = 2Ro = √3).
Сечение S = (1/2)H*(2Ro) = (1/2)*(3/2)*√3 = 3√3/4.
Получаем Rш = (√3*√3*√3)/(4*(3√3/4)) = 1.
Объём шара V = (4/3)πR³ = (4/3)π куб
Объяснение:
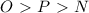- всё это конечно углы.
Объяснение:
По условию угол 1 равен 30 градусам . Градусная мера развернутого - 180 градусов . По рисунку сразу определяем угол 3 . Он равен 180 градусов - 30 градусов = 150 градусов . Дальше по условию видим , что угол 1 равен углу 2 , а угол 3 , равен углу 4 . Средовательно угол 3 , 4 равен 150 градусов , а угол 1 и 2 - 30 градусов .
Делаем проверку . Тут дана окружность . Градусная мера окружности равна 360 градусов . Делаем проверку : 150 + 150 + 30 + 30 равно 360 . Задача решена )))