(26;4)
Объяснение:
Так как наши графики являются прямыми, функции выглядят так: 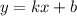
Найдем значения k и b, подставив значения точек A и B в уравнение 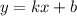 и решив следующую систему:
и решив следующую систему:
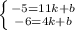
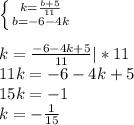
Найдем b, подставив в 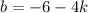 :
:
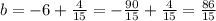
Первое уравнение имеет такой вид: 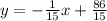
- - - - - -
Найдем второе уравнение по аналогии (мне лень расписывать системами, так что я буду писать просто через новую строчку и в конце запишу итоговое решение системы)
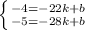
- - - - -
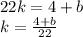
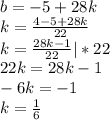
- - - - -
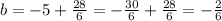
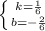
Второе уравнение имеет следующий вид: 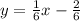
Чтобы найти точку пересечения, нужно приравнять уравнения графиков.
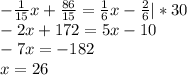
Чтобы найти y, нужно подставить в любое уравнение значение x.
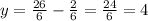
ответ: (26;4)
242
Объяснение:
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её 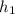 ). Тогда справедливо следующее равенство:
). Тогда справедливо следующее равенство:
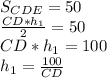
Аналогично в треугольнике ABE:
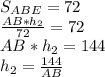
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
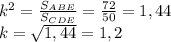
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
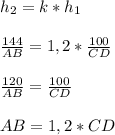
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме 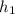 и
и 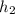 , то есть
, то есть
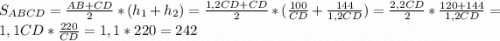
Объяснение:
2) Р=2х+х-8=х-8=31
х=39
3)Т.к. АВ=5 и ВН- высота и АН=НС,то треугольник АВС - равнобедренный.
Значит Р=5+5+3+3=16
4) Правильные:
а) Соответственные углы равны
б)Соответственные углы в сумме дают 180°, если прямая А перпендикулярна С и прямая Б перпендикулярна С
г)Внутренние накрест лежащие углы равны
5)х+4х+4х=180°
9х=180°
х=20°
Угол при основании равен 4*20°=80°