Объяснение:
Раз нам даны точки в пространстве, то скорее всего с векторами уже знакомы, тогда. Найдем векторы АВ и ВС, для этого нужно от координат конца отнять соответствующие координаты начала, тогда
(в)АВ(-5-2;4-5;-4-(-1))=(-7;-1;-3)
(в)BC(1-(-5);-2-4;2-(-4))=(6,-6,6)
По определению параллелограма это четырехугольник у которого 2 пары параллельных равных сторон, сделовательно (в)AB=(в)CD
(в)AB(-7;-1;-3), C(1;-2;2) Пусть точка D имеет координаты x,y,z. Следовательно (в)CD(x-1;y+2;z-2) и эти выражения x-1;y+2;z-2 соответственно равны -7;-1;-3. Тогда
x-1=-7⇔x=-6
y+2=-1⇔y=-3
z-2=-3⇔z=-1. Следовательно координаты точки D(-6,-3,-1)
Так как диагональ точкой пересечения делится пополам, то точка пересечения диагоналей это середина диагонали, диагональ - отрезок соединяющий 2 несоседние вершины, значит найдем середину BD или АС
Координаты середины отрезка находятся по формуле среднего арифмитеческого соответствующих координат концов, т.е. абсцисса первой точки+ абсцисса второй точки делить на 2, ордината и апликата соответственно, тогда
Середина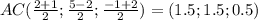 
Точка с этими координатами,пусть точка О, и есть точка пересечения диагоналей.
Длина AB .длина вектора это есть квадратный корень из суммы квадратов его координат, тогда длина АВ = длине вектора АВ
|(в)АВ|=
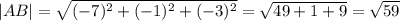
BC=2√2, ∠А=45°,∠B=45°
Объяснение:
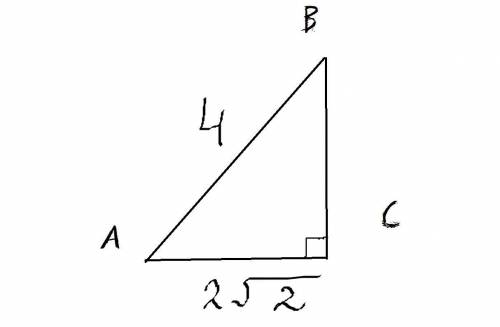
Решить треугольник - значит найти все неизвестные элементы.
Мы имеем прямоугольный треугольник. Также нам известны две его стороны. Это значит, что мы можем воспользоваться теоремой Пифагора, чтобы найти оставшуюся сторону:
ВС²=АB² - AC²
BC²=4² - (2√2)² = 16 - 4·2 = 16 - 8 = 8
BC = √8 = √4·2 = 2√2
Замечаем, что BC и АС равны 2√2. Это значит, что наш треугольник не только прямоугольный, но еще и равнобедренный. Значит, остальные его углы равны по 45° (т.к. общая сумма углов треугольника 180, а один из углов 90. Значит остальные два угла 90:2=45).
ответ: BC=2√2, ∠А=45°,∠B=45°
Меньшая диагональ, а значит и высота пирамиды, находится по теореме косинусов:
h^2 = 4 + 3 - 2*2*√3 *cos30 = 7 - 6 = 1. h = 1 cm.
Площадь основания:
Sосн = 2*√3 *sin30 = √3 см^2
Объем пирамиды:
V = (1/3)Sосн*h = √3 /3 cm^3