Два угла треугольника равны 40° и 52°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов.
- - -
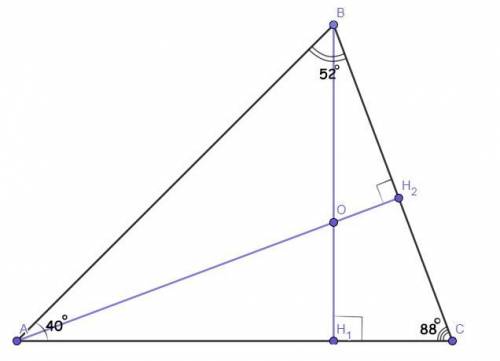
Дано :ΔАВС.
∠А = 40°.
∠В = 52°.
ВН₁ и АН₂ - высоты.
Точка О - ортоцентр (точка пересечения высот).
Найти :∠АОВ = ? (или ∠Н₁ОН₂, не важно, так как они равны как вертикальные).
Решение :Немного о расположении ортоцентра О :
Для начала найдём ∠С.
По теореме о сумме углов треугольника -
∠А + ∠В + ∠С = 180°
∠С = 180° - ∠А - ∠В
∠С = 180° - 40° - 52°
∠С = 88°.
Так как все углы ΔАВС - острые, то ортоцентр О лежит внутри ΔАВС.
- - -
Рассмотрим ΔСВН₁ - прямоугольный (так как ∠ВН₁С = 90° по определению высоты треугольника).
Сумма острых углов прямоугольного треугольника равна 90°.Тогда -
∠Н₁СВ + ∠Н₁ВС = 90°
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - 88°
∠Н₁ВС = 2°.
Теперь рассмотрим ΔОВН₂ - прямоугольный (так как ∠ОН₂В = 90°).
По выше сказанному -
∠ВОН₂ + ∠ОВН₂ = 90°
∠ВОН₂ = 90° - ∠ОВН₂
∠ВОН₂ = 90° - 2°
∠ВОН₂ = 88°.
- - -
∠ВОН₂ и ∠АОВ - смежные.
Сумма смежных углов равна 180°.Следовательно -
∠ВОН₂ + ∠АОВ = 180°
∠АОВ = 180° - ∠ВОН₂
∠АОВ = 180° - 88°
∠АОВ = 92°.
ответ :92°.
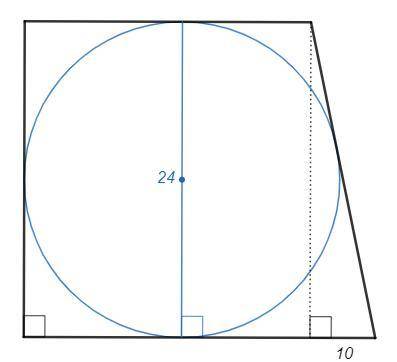
Диаметр, проведенный в точку касания, перпендикулярен касательной. Диаметр перпендикулярен основаниям трапеции и является ее высотой. Высота равна 24.
Опустим высоту из вершины меньшего основания. Она разделит трапецию на прямоугольник и прямоугольный треугольник. Противоположные стороны прямоугольника равны, таким образом катет треугольника равен 10.
Найдем боковую сторону трапеции как гипотенузу по теореме Пифагора.
√(10^2 +24^2) =26
(Или пифагорова тройка 5, 12, 13, множитель 2: 13*2=26)
Боковая сторона, перпендикулярная основаниям, равна высоте, 24.
В описанном четырехугольнике суммы противоположных сторон равны.
P=2(24+26) =100
1)
<ABC=90°, т.к. в данном треугольнике есть один прямой угол.
2)
<ABC=50°
180°- 130°=50°