1) обозначим угол CAD = x, тогда угол DAB = x, так как АД- биссектриса
и угол АСД = y
2) так как АС=АД и АД=ДВ из условия, то треугольники АСД и АДВ равнобедренные
3) так как треугольники АСД и АДВ равнобедренные, то углы САД=ДАВ=АВД=х,
АСД=АДС=у
4) сумма углов треугольника = 180 градусов и сумма смежных углов = 180 градусов, значит выразим угол АДВ=180-2х=180-у. решаем равенство, находим зависимость у от х: у=2х
5) рассмотрим треугольник АСД: х+2у=х+2х+2х=5х=180; 5х=180; х=36 (градусов)
тогда у= 36*2=72 градуса
6) угол А = САД=ДАВ=2х=72 градуса
угол В = х = 36 градусов
угол С = АСД = у=2х= 72 градуса
ОТВЕТ: 72, 36, 72
Дано: АВСД - трапеция, АВ=СД, АД=16√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=1\2 АД=16√3:2=8√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=16√3:2=8√3;
АС²=(16√3)²-(8√3)²=768-192=576; АС=√576=24.
СН=1\2 АС=24:2=12.
S(АВСД)=(8√3+16√3):2*12=144√3 (ед²).
ответ: 144√3 ед²
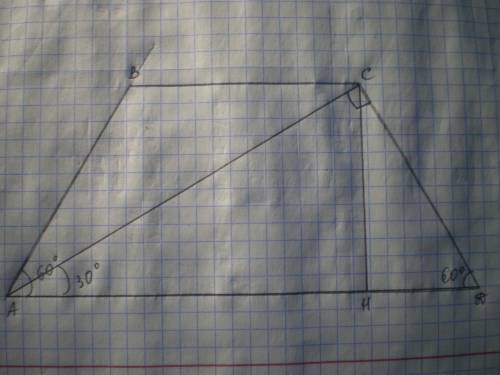
Дано: АВСД - трапеция, АВ=СД, АД=16√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=1\2 АД=16√3:2=8√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=16√3:2=8√3;
АС²=(16√3)²-(8√3)²=768-192=576; АС=√576=24.
СН=1\2 АС=24:2=12.
S(АВСД)=(8√3+16√3):2*12=144√3 (ед²).
ответ: 144√3 ед²

Это ОЧЧЕНЬ хороший треугольник, потому что из него можно легко найти выражение для тригонометрических функций углов, кратных pi/10 (то есть 18 градусов);
Пусть угол DAC = Ф;
Тогда
угол BAD = Ф; (AD - биссектриса)
угол ABD = Ф; (треугольник ADB равнобедренный)
угол ADC = угол DAB + угол ABD = 2*Ф; (внешний угол треугольника)
угол ACD = угол ADC = 2*Ф; (треугольник ADС равнобедренный)
Итак, в треугольнике ADC углы Ф, 2*Ф и 2*Ф. Остюда Ф = pi/5 = 36 градусов.
Само собой, что в треугольнике АВС углы при основании 2*Ф = 72 градуса, угол при вершине 36 градусов.
Треугольник АВС равнобедренный - при решении мы этим нигде не пользовались, это само так получилось.