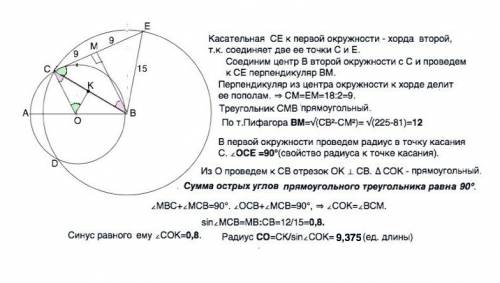
Касательная СЕ к первой окружности - хорда второй, т.к. соединяет две ее точки С и Е.
Соединим центр В второй окружности с С и проведем к СЕ перпендикуляр ВМ.
Перпендикуляр из центра окружности к хорде делит ее пополам. ⇒ СМ=ЕМ=18:2=9. Треугольник СМВ прямоугольный.
По т.Пифагора ВМ=√(СВ²-СМ²)= √(225-81)=12
В первой окружности проведем радиус в точку касания С. ∠ОСЕ =90°(свойство радиуса к точке касания).
Из О проведем к СВ отрезок ОК ⊥ СВ. ∆ СОК - прямоугольный. Сумма острых углов прямоугольного треугольника равны 90°.
∠МВС+∠МСВ=90°. ∠ОСВ+∠МСВ=90°, ⇒ ∠СОК=∠ВСМ. sin∠МСВ=МВ:СВ=12/15=0,8. Синус равного ему ∠СОК=0,8.
Радиус СО=СК/sin∠COK= 9,375 (ед. длины)
Касательная СЕ к первой окружности - хорда второй, т.к. соединяет две ее точки С и Е.
Соединим центр В второй окружности с С и проведем к СЕ перпендикуляр ВМ.
Перпендикуляр из центра окружности к хорде делит ее пополам. ⇒ СМ=ЕМ=18:2=9. Треугольник СМВ прямоугольный.
По т.Пифагора ВМ=√(СВ²-СМ²)= √(225-81)=12
В первой окружности проведем радиус в точку касания С. ∠ОСЕ =90°(свойство радиуса к точке касания).
Из О проведем к СВ отрезок ОК ⊥ СВ. ∆ СОК - прямоугольный. Сумма острых углов прямоугольного треугольника равны 90°.
∠МВС+∠МСВ=90°. ∠ОСВ+∠МСВ=90°, ⇒ ∠СОК=∠ВСМ. sin∠МСВ=МВ:СВ=12/15=0,8. Синус равного ему ∠СОК=0,8.
Радиус СО=СК/sin∠COK= 9,375 (ед. длины)

Объяснение:
S=ah
S=1/2×22×15= 165 см²
2
S=1/2 ab=1/2×9×4=18 см²
3
CB=1/2AB=1/2×20= 10 см
S=1/2CB×AC=1/2×10×12=60 см²
4
26²=2AC²
AC²=676/2=338
S=1/2×338=169 см²
5
AC=8 см ,HC=1/2AC=1/2×8=4 см,
<HBC=1/2<B=1/2×60°=30°
BC=2HC=2*4=8 см
BH=√BC²-HC²=√8²-4²=√64-16=√48=4√3 см
S=1/2BH×AC=1/2×4√3×8=16√3 см²
6
<BMC=180°-<BMA=180°-135°=45°
BC=MC= 10 см
AC=AM+MC=6+10=16 см
S=1/2AC×BC=1/2×16×1O=80 см²
8
p=(13+14+15)÷2=21 см
S = √p(p - a)(p - b)(p - c)=√21(21 - 13)(21 - 14)(21- 15)=√21×8×7×6=√7056=84 см²